
����Ŀ����ͼ1����ABC�ı�BC��ֱ��l�ϣ�AC��BC����AC=BC����EFP�ı�FPҲ��ֱ��l�ϣ���EF���AC�غϣ���EF=FP��
��1��ֱ��д��AB��AP�������������ϵ��_____��AB��AP��λ�ù�ϵ��_____��
��2������ABC��ֱ��l����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ����֤��AP=BQ��
��3������ABC��ֱ��l����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ����̽��AP=BQ�Ƿ��Գ�������˵�����ɣ�

���𰸡���1��AB=AP��AB��AP����2��֤������������3�����������ɼ�����.
�������������������1��AB=AP��AB��AP����֪AC��BC��AC=BC���ɵ���ABCΪ����ֱ�������Σ�������BAC=��ABC=45����������֪������֤��PEF=45�������ɵ���BAP=90�������۵�֤����2��������֪������֤Rt��BCQ��Rt��ACP������ȫ�������ε����ʼ��ɵý�������3�������Գ�������ȣ�2������֤�����ɣ�
���������
��1��AB=AP��AB��AP��
֤������AC��BC��AC=BC��
���ABCΪ����ֱ�������Σ�
���BAC=��ABC=![]() ��180�㩁��ACB��=45����
��180�㩁��ACB��=45����
��֪����ABC�ա�EFP��
ͬ����֤��PEF=45����
���BAP=45��+45��=90����
��AB=AP��AB��AP��
�ʴ�Ϊ��AB=AP AB��AP
��2��֤����
��EF=FP��EF��FP
���EPF=45����
��AC��BC��
���CQP=��EPF=45��
��CQ=CP
�� Rt��BCQ��Rt��ACP��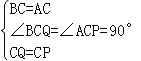
��Rt��BCQ��Rt��ACP ��SAS����
��AP=BQ��
��3��AP=BQ�������������£�
��EF=FP��EF��FP��
���EPF=45����
��AC��BC
���CPQ=��EPF=45��
��CQ=CP
�� Rt��BCQ��Rt��ACP��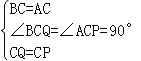
��Rt��BCQ��Rt��ACP ��SAS����
��AP=BQ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCD�����Σ�AD=5,����D��AB�Ĵ���DH,����ΪH,���Խ���AC��M������BM����AH=3��
��1����֤:DM=BM��
��2����MH�ij���
��3����ͼ2������P�ӵ�A������������ABC������2����λ������ٶ����յ�C�����˶�������PMB�����ΪS��S��0������P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��
��4���ڣ�3���������£�����P�ڱ�AB���˶�ʱ�Ƿ���������� tֵ��ʹ��MPB����BCD��Ϊ��ǣ�������,�����tֵ��������������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵���� ��abc��0��
��2a��b=0��
��4a+2b+c��0��
��������5��y1������ ![]() ��y2���������������㣬��y1��y2 ��
��y2���������������㣬��y1��y2 ��
����˵����ȷ���ǣ� ��
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪б��AB��Ϊ80�ף��½ǣ�����BAC��Ϊ30�㣬BC��AC���ּƻ���б���е�D����ȥ�������壨����Ӱ��ʾ����һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��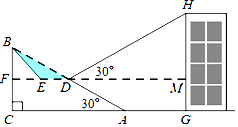
��1��������б��BE���½�Ϊ45�㣬��ƽ̨DE�ij���������������ţ�
��2��һ��������GH����A��36��Զ����AGΪ36�ף���С����D����ý����ﶥ��H�����ǣ�����HDM��Ϊ30�㣮��B��C��A��G��H��ͬһ��ƽ���ڣ���C��A��G��ͬһ��ֱ���ϣ���HG��CG��������GH�ĸ߶ȣ�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼһ��������y=ax2+bx+c��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=x��2����A��C���㣬��AB=2��
��1���������ߵĽ���ʽ��
��2����ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶�������ͼ2��������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��s= ![]() ����tΪ��ֵʱ��s����Сֵ���������Сֵ��
����tΪ��ֵʱ��s����Сֵ���������Сֵ��
��3���ڣ�2���������£��Ƿ����t��ֵ��ʹ��P��B��DΪ��������������ABC���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��D��C��F��ͬһ��ֱ���ϣ�AB=DE��BC=EF��Ҫʹ��ABC�ա�DEF������Ҫ����һ�������ǣ�������

A. ��BCA=��F�� B. ��B=��E�� C. BC��EF �� D. ��A=��EDF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2004��8��1����,�㽭ʡ������������õ�ִ���µĵ������:��װ��һ��һ�����ľ���
�û�,���ó�������(ÿ���û��������ʾ���õ���)ʵ�н���ʽ�۽��Ӽ�,���е���50ǧ��ʱ(��50
ǧ��ʱ)���ֵ�۲�����;51��200ǧ��ʱ����ÿǧ��ʱ����ϵ�0.03Ԫ;����200ǧ��ʱ����ÿǧ
��ʱ����ϵ�0.10Ԫ.��֪����ǰ���ͳһΪÿǧ��ʱ0.53Ԫ.
��1��������ʦ��10�·ݵ��õ���Ϊ130ǧ��ʱ,��10�·�����ʦ��Ӧ����Ѷ���Ԫ?
��2����֪����ʦ��10�·ݵ��õ���Ϊ![]() ǧ��ʱ,������������:
ǧ��ʱ,������������:
����![]() ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ;
ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ;
����50��![]() ��200ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ;
��200ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ;
����![]() ��200ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ.
��200ǧ��ʱ,��10�·�����ʦ��Ӧ�����Ϊ Ԫ.
��3����10�·�����ʦ��Ӧ�����Ϊ96.50Ԫ,��10�·�����ʦ�ҵ��õ����Ƕ���ǧ��ʱ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����ֱ��CD����һ��P��

��1�����P����C��D֮���˶�ʱ������PAC����APB����PBD��������������ϵ����˵�����ɣ�
��2������P��C��D���������˶�ʱ��P�����C��D���غϣ�����̽����PAC����APB����PBD֮��Ĺ�ϵ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�� ![]() ������A��B��ֱ��l��ÿ��1����λ���ٶ�����������ƽ���˶������ͬʱ����P�ӵ�B��������ֱ��l����ÿ��1����λ���ٶ���ֱ��l�����·����������˶����������˶���ʱ��Ϊt�룮
������A��B��ֱ��l��ÿ��1����λ���ٶ�����������ƽ���˶������ͬʱ����P�ӵ�B��������ֱ��l����ÿ��1����λ���ٶ���ֱ��l�����·����������˶����������˶���ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��2����O��OC��AB��C����C��CD��x����D���ʣ�tΪ��ֵʱ����PΪԲ�ġ�1Ϊ�뾶��Բ��ֱ��OC���У���˵����ʱ��P��ֱ��CD��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com