
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
【答案】∠APB=∠PBD-∠PAC或∠APB=∠PAC-∠PBD
【解析】试题分析:(1)过点P作PE∥l1根据l1∥l2得出PE∥l2∥l1,从而得出∠PAC=∠1,∠PBD=∠2,然后得出答案;(2)分点P在C、D两点的外侧运动,在l1上方和在l2下方时两种情况,分别根据(1)的方法得出答案.
试题解析:(1)当点P在C、D之间运动时,∠APB=∠PAC+∠PBD.理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)ⅰ)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
ⅱ)当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为 . 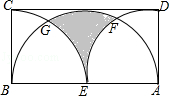
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________,∠3=________;
(2)在(1)中,若∠1=55°,则∠3=________;若∠1=40°,则∠3=________;
(3)由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3=________时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
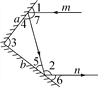
查看答案和解析>>
科目:初中数学 来源: 题型:
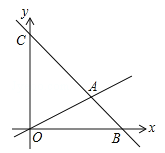
【题目】如图,在平面直角坐标系中,直线![]() 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
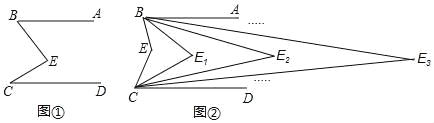
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=![]() ∠BEC;
∠BEC;
(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC. 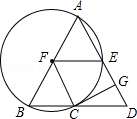
(1)求证:GC是⊙F的切线;
(2)填空: ①若∠BAD=45°,AB=2 ![]() ,则△CDG的面积为 .
,则△CDG的面积为 .
②当∠GCD的度数为时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
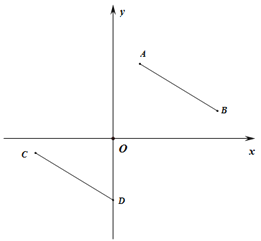
【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足![]() +(a+b-7)2=0.
+(a+b-7)2=0.
(1) 求a、b的值;
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com