
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
【答案】 (1)证明见解析;(2)猜测:PE=QE.证明见解析; (3)S△DEP =![]() .
.
【解析】试题分析:本题是一道几何证明题,主要考查了正方形的性质、全等三角形的性质与判定、勾股定理等知识点,试题难度不大,但要注意第(3)题中认真计算,避免出错.
求证DP=DQ;只需证明△ADP≌△CDQ即可得到DP=DQ.解题的关键是找出∠PDC的两个余角相等即∠ADP =∠CDQ,两三角形全等的条件就具备了.
PE=QE.只需证明△PDE≌△QDE即可得到,由(1)的结论DP=DQ加上DE是∠PDQ的平分线易用SAS证得结论.
(3)由AB:AP=3:4,AB=6可求AP=8,BP=2;直接由(1)和(2)的结论AP=CQ、PE=QE设CE=x,则PE=8-x,利用勾股定理求得Rt△PEB的边PE,由此可得EQ的长度,这样△DEP的面积就不难求得了.
试题解析:
(1)证明:∵四边形ABCD是正方形
∴DA=DC,∠DAP=∠DCQ=90°
∵∠PDQ=90°
∴∠ADP+∠PDC=90°
∠CDQ+∠PDC=90°
∠ADP=∠CDQ
在△ADP与△CDQ中
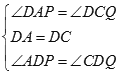
∴△ADP≌△CDQ(ASA)
∴DP=DQ
(2)解:PE=QE.证明如下:
∵ DE是∠PDQ的平分线
∴∠PDE=∠QDE
在△PDE与△QDE中

∴△PDE≌△QDE(SAS)
∴PE=QE
(3)解:∵AB:AP=3:4,AB=6
∴AP=8,BP=2,
由(1)知:△ADP≌△CDQ 则AP=CQ=8
由(2)知:△PDE≌△QDE,PE=QE
设CE=x,则PE=QE=CQ-CE=8-x
在Rt△PEB中,BP=2,BE=6+x,PE=8-x
由勾股定理得:22+(6+x)2=(8-x)2
解得:x=![]()
∴![]()
![]()
∴△DEP的面积为:![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
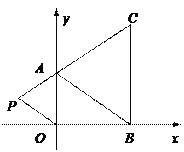
【题目】如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)、(b,c),其中a,b,c满足关系式(3a-2b)2+![]() =0,|c-4|≥0.
=0,|c-4|≥0.
⑴求a,b,c的值;
⑵如果在第二象限内有一点P(m-1,1),请用含m的代数式表示△AOP的面积;
⑶在⑵的条件下,m在什么范围取值时,△AOP的面积不大于△ABC的面积?请求出在符合条件的前提下、△AOP的面积最大时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | |
| | 2 | | 4 | | 2 | |
| m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= ![]() 的一条性质: .
的一条性质: .
(5)如果方程 ![]() =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据解答过程填空:

如图,已知 ![]() ,那么AB与DC平行吗?
,那么AB与DC平行吗?
解: ![]() 已知
已知 ![]()
![]() ________
________ ![]() ________(________ )
________(________ )
![]() (_______ )
(_______ )
又 ![]() (________ )
(________ )
![]() ________
________ ![]() 等量代换
等量代换 ![]()
![]() (________ )
(________ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )
A.m< ![]()
B.m> ![]() 且m≠2
且m≠2
C.m≤ ![]()
D.m≥ ![]() 且m≠2
且m≠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com