
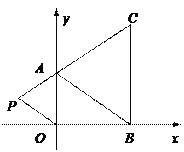
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��B��C���������ֱ�Ϊ(0��a)(b��0)��(b��c)������a��b��c�����ϵʽ(3a��2b)2��![]() ��0��|c��4|��0��
��0��|c��4|��0��
����a��b��c��ֵ��
������ڵڶ���������һ��P(m��1��1)�����ú�m�Ĵ���ʽ��ʾ��AOP�������
���ڢƵ������£�m��ʲô��Χȡֵʱ����AOP����������ڡ�ABC�������������ڷ���������ǰ���¡���AOP��������ʱ��P�����꣮
���𰸡���1����a��2��b��3��c��4�� ��2��S��AOP��1��m����3��P�������Ϊ(��6��1).
����������1���ɷǸ������ʶ����ɵ� ���ⷽ����ɵ�a,b,c��
���ⷽ����ɵ�a,b,c��
��2����ϵ�A,P,O�����꣬���������������ʽ�ɵõ�S��AOP��1��m��
��3���ֱ���ʽ�ӱ�ʾ���������ε�����������á���AOP����������ڡ�ABC��������͵�P�ڵڶ����ޣ��г�����ʽ�������m��ȡֵ��Χ���ٸ�������ȷ��m=-5ʱ����AOP����������P�����꣮
![]()
��c��4=0��
��a��2��b��3��c��4��
��S��AOP��1��m��
�������ã�B(3��0)��C(3��4)��
��|BC|��4����A��BC�ľ���Ϊ3��
��S��ABC��![]() ��3��4��6��
��3��4��6��
�ߡ�AOP�������������ABC�������S��AOP��1��m��
��S��AOP��S��ABC��S��AOP��1��m��
��1��m��6�����m�ݣ�5����
����P(m��1��1)�ڵڶ������ڣ�
��m��1��0��m��1��
�����١�����֪����5��m��1
����5��m��1ʱ����AOP�������������ABC�������
��S��AOP��1��m����5��m��1
����m����5ʱ����ʱ��AOP��������S��AOP��1��m��6��
��P�������Ϊ(��6��1).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��y=x�� ![]() ��x�������ᡢy�Ḻ����ֱ��ཻ��A��C���㣬������y=
��x�������ᡢy�Ḻ����ֱ��ཻ��A��C���㣬������y= ![]() x2+bx+c������B����1��0���͵�C��
x2+bx+c������B����1��0���͵�C��
��1����գ�ֱ��д�������ߵĽ���ʽ����
��2����֪��Q��������y= ![]() x2+bx+c�ڵ��������ڵ�һ�����㣮
x2+bx+c�ڵ��������ڵ�һ�����㣮
����ͼ������AQ��CQ�����Q�ĺ�����Ϊt����AQC�����ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
������BQ��AC�ڵ�D������BC����BDΪֱ������I���ֱ�BC��AB�ڵ�E��F������EF�����߶�EF����Сֵ����ֱ��д����ʱQ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BC=4���Զ���A��BΪԲ�ģ���AD��BC��Ϊ�뾶�������������������ڵ�E����E��AB�ϣ���ABΪֱ������Բǡ����DC���У���ͼ����Ӱ���ֵ����Ϊ �� 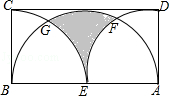
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ǵ�ĸ�ӣ��������Ϊ�˴����ؽ��羰�������ο��ã���һ�γ�Ϊ180���ؽ��ӵ�����������A��B�����̶��Ⱥ������ɣ�A������ÿ������12�ף�B���̶�ÿ������8�ף�����ʱ20�죮��A��B�����̶ӷֱ����κӵ������ף�
�Ÿ������⣬�ߢŰ��ͬѧ�г��в������ķ��������¡����ݼ�ͬѧ���еķ����飬����ֱ�ָ��δ֪��x��y��ʾ�����壬Ȼ���ڷ����в�ȫ��ͬѧ���еķ����飻
![]() ��x��ʾ________________________��y��ʾ_________________________��
��x��ʾ________________________��y��ʾ_________________________��
�������ͬѧֱ����A���̶����κӵ�������Ϊx��B���̶����κӵ�������Ϊy���г���һ�������飬��A��B�����̶ӷֱ����κӵ������ף����������д�������Ľ����̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����P��x��y��������x��y��Ϊ��������Ƶ�PΪ��㣬��һ������ε������ΪS�����ڲ��ĸ������ΪN���߽��ϵĸ������ΪL������ͼ�С�ABC�Ǹ�������Σ���Ӧ��S=1��N=0��L=4��
��1�����ͼ�и���ı���DEFG��Ӧ��S��N��L��
��2����֪������ε�����ɱ�ʾΪS=N+aL+b������a��bΪ��������ij������ζ�Ӧ��N=82��L=38����S��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O�����ߣ�BΪ�е㣬Բ����AC�ϣ���A=30�㣬DΪ ![]() ���е㣮
���е㣮 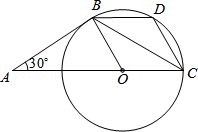
��1����֤��AB=BC��
��2����֤���ı���BOCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�����߶�������ĸ��Ƕ���ֱ�ǵ��ı��ν��������Ρ���У�������߰�����ѧ��ȤС�鿪չ��һ�ο������������£���ͼ�٣�������ABCD�У�AB=6�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ�����D���غϣ����ǰ��һ�߽�AB�ڵ�P����һ�߽�BC���ӳ����ڵ�Q��

��1����֤��DP=DQ��
��2����ͼ�ڣ�С����ͼ1�Ļ���������PDQ��ƽ����DE��BC�ڵ�E������PE��������PE��QE����һ����������ϵ����²����Ľ��۲�����֤����
��3����ͼ�ۣ��̶����ǰ�ֱ�Ƕ�����D�㲻����ת�����ǰ壬ʹ���ǰ��һ�߽�AB���ӳ����ڵ�P����һ�߽�BC���ӳ����ڵ�Q��������PDQ��ƽ����DE��BC�ӳ����ڵ�E������PE����AB��AP=3��4�����С�������DEP�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��֤����ƽ�澵������ߵĹ����ǣ��䵽ƽ�澵�ϵĹ��ߺͱ�������Ĺ�����ƽ�澵���е������ȣ�
(1)��ͼ��һ������m�䵽ƽ�澵a�ϣ���a���䵽ƽ�澵b�ϣ��ֱ�b�����䣮����b������Ĺ���n�����mƽ�У��ҡ�1=50�������2=________����3=________��
(2)��(1)������1=55�������3=________������1=40�������3=________��
(3)��(1)��(2)������룺����ƽ�澵a��b�ļнǡ�3=________ʱ������ʹ�κ��䵽ƽ�澵a�ϵĹ���m������ƽ�澵a��b�����η�����������m�뷴�����nƽ�У���˵�����ɣ�
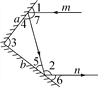
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABD�У�AB=AD����ABΪֱ���ġ�F��BD�ڵ�C����AD�ڵ�E��CG��AD�ڵ�G������FE��FC�� 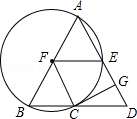
��1����֤��GC�ǡ�F�����ߣ�
��2����գ� ������BAD=45�㣬AB=2 ![]() �����CDG�����Ϊ ��
�����CDG�����Ϊ ��
�ڵ���GCD�Ķ���Ϊʱ���ı���EFCD�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com