
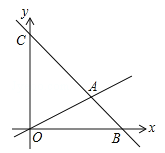
【题目】如图,在平面直角坐标系中,直线![]() 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.
【答案】(1)点B的坐标为(6,0),点C的坐标为(0,6);(2)12;(3)M的坐标是:M(1, ![]() )或M(1,5)或(﹣1,7)
)或M(1,5)或(﹣1,7)
【解析】试题分析:(1)在y=-x+6中, 分别令x=0,y=0即可得到结论;
(2)根据三角形面积公式计算即可;
(3)根据三角形的面积公式可判断M的横坐标是1,然后把x=1分别代入OA和AC的解析式中计算对应的函数值即可得到M点的坐标.
试题解析:解:(1)设y = 0,则x = 6;设x = 0,则y = 6,故点B的坐标为(6,0),点C的坐标为(0,6);
(2)S△OAC = ![]() OC×xA=
OC×xA=![]() ×6×4 =12;
×6×4 =12;
(3)存在点M使S△OMC=![]() S△OAC.
S△OAC.
设M的坐标为(x,y);OA的解析式是y=mx,则4m =2,
解得:m=![]() ,则直线OA的解析式是:y=
,则直线OA的解析式是:y=![]() x.
x.
∵当S△OMC= ![]() S△OAC时,即
S△OAC时,即![]() ×OC×|x|=
×OC×|x|=![]() ×12.
×12.
又∵OC=6,∴x =±1.
①当M在线段OA上时,x>0,所以x=1时,y=![]() ,则M的坐标是(1,
,则M的坐标是(1, ![]() );
);
②当M在射线AC:y=﹣x+6上时,由x=1,得y=5,则M的坐标是(1,5);由x=-1,得y=7,则M的坐标是(-1,7).

综上所述:M的坐标是:M(1, ![]() )或M(1,5)或(﹣1,7).
)或M(1,5)或(﹣1,7).


科目:初中数学 来源: 题型:
【题目】某校七年级三班为配合国家级卫生城市创建验收,自愿组织参加环卫整治活动,学校用两张统计图公布了该班学生参加本次活动的情况.小明、小华、小丽三个同学看了这张统计图后,小明说:“该班共有25名学生参加了本次活动”小华说:“该班参加美化数目的学生占参加本次活动人数的40%”小丽说:“该班有6名学生清扫道路.”小明、小华、小丽三人说法正确的有( )
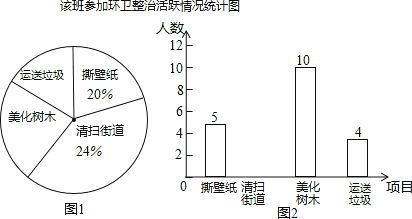
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | |
| | 2 | | 4 | | 2 | |
| m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= ![]() 的一条性质: .
的一条性质: .
(5)如果方程 ![]() =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积 . 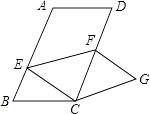
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.
(1)求A、B两种型号的轿车每辆分别多少元?
(2)若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN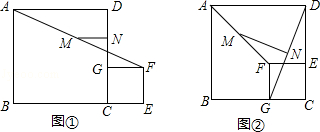
(1)线段MN和GD的数量关系是 , 位置关系是;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)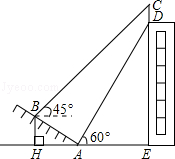
(1)求点B距水平而AE的高度BH;
(2)求宣传牌CD的高度.
(结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com