
【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足![]() +(a+b-7)2=0.
+(a+b-7)2=0.
(1) 求a、b的值;
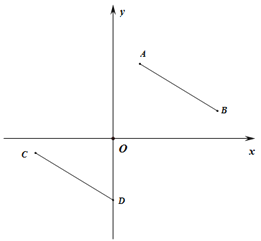
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
【答案】(1)![]() ;(2)D(0,
;(2)D(0,![]() );(3)当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.
);(3)当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.
【解析】
(1)由a、b满足![]() +(a+b-7)2=0可得:2a-b-2=0,a+b-7=0,由这两个等式组成关于a、b的方程组,解此方程组即可求得a、b的值;
+(a+b-7)2=0可得:2a-b-2=0,a+b-7=0,由这两个等式组成关于a、b的方程组,解此方程组即可求得a、b的值;
(2)如下图,分别过点A,B作AE⊥y轴E, BF⊥y轴F,由S平行四边形ABDC=20可得S△ABD= S四边形AEFB+S△BFD- S△AFD=10,因此结合图形和题意列出关于n的方程,解方程求得n的值即可得到点D的坐标;
(3)设旋转后直线AB′与DC′交于点E,过点E作直线EF∥AB,则可得: EF∥AB∥CD,然后分∠AEC′=60°,∠AED=60°,∠B′EC′=60°三种情况结合图1、图2和图3及已知条件进行分析解答即可.
(1)∵a、b满足![]() +(a+b-7)2=0,
+(a+b-7)2=0,
∴![]() ,解得:
,解得:![]() ;
;
(2)分别过点A,B作AE⊥y轴E, BF⊥y轴F,
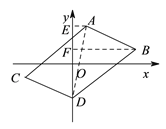
∵S平行四边形ABDC=20,
S△ABD= S四边形AEFB+S△BFD- S△AFD,
又∵A(1,3),B(4,1),D(0,n),
∴S△ABD=![]() =10, 解得
=10, 解得![]()
∴点 D的坐标为(0,![]() );
);
(3)设旋转后直线AB′与DC′交于点E,过点E作直线EF∥AB,
∵AB∥CD,
∴ EF∥AB∥CD.
①如图1,若∠AEC′=60°,
∵EF∥AB∥CD,
∴∠AEF=∠BAB′=8t,∠FEC′=∠CDC′=2t,
∴∠AEC′=8t-2t=60°,解得t=10;

②如图2,若∠AED=60°,
∵EF∥AB∥CD,
∴∠AEF+∠BAB′=180°,∠FED=∠CDC′=2t,
∴∠AEF=180°-8t,
∵∠AED=∠AEF+∠FED=60°,
∴180°-8t+2t=60°,解得:t=20;
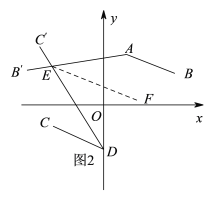
③如图3,若∠B′EC′=60°,
∵EF∥AB∥CD,
∴∠FEB′=∠BAB′=360°-8t,∠FED=∠CDC′=2t,
∵∠B′EC′=180°-∠FEB′-∠FED=60°,
∴180°-(360-8t)-2t=60°,解得:t=40;

综上所述,当t为10秒,20秒或40秒时,直线AB与直线CD的夹角为60°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )
A.m< ![]()
B.m> ![]() 且m≠2
且m≠2
C.m≤ ![]()
D.m≥ ![]() 且m≠2
且m≠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,……如此继续运动下去.设Pn(xn,yn),n=1、2、3、……,则x1+x2+……+x2014+x2015的值为( )

A. 1 B. 3 C. -1 D. 2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)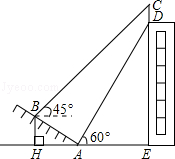
(1)求点B距水平而AE的高度BH;
(2)求宣传牌CD的高度.
(结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如下表:
甲 | 1 | 1 | 0 | 2 | 1 | 3 | 2 | 1 | 1 | 0 |
乙 | 0 | 2 | 2 | 0 | 3 | 1 | 0 | 1 | 3 | 1 |
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果来看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中, ![]() ,点E是边BC上的动点
,点E是边BC上的动点![]() 不与点
不与点![]() 重合
重合![]() ,以AE为边作
,以AE为边作![]() ,使得
,使得![]() ,射线AF交边CD于点F.
,射线AF交边CD于点F.
![]() 如图1,当点E是边CB的中点时,判断并证明线段
如图1,当点E是边CB的中点时,判断并证明线段![]() 之间的数量关系;
之间的数量关系;
![]() 如图2,当点E不是边BC的中点时,求证:
如图2,当点E不是边BC的中点时,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() ,
, ![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() .
.

求证: ![]() .
.
证明:在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() ( ).
( ).
∴![]() __________
__________![]() __________( ).
__________( ).
∴![]() 是
是![]() 的角平分线.
的角平分线.
又∵![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
∴![]() ( ).
( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com