
【题目】在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,……如此继续运动下去.设Pn(xn,yn),n=1、2、3、……,则x1+x2+……+x2014+x2015的值为( )

A. 1 B. 3 C. -1 D. 2015
科目:初中数学 来源: 题型:
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
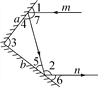
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________,∠3=________;
(2)在(1)中,若∠1=55°,则∠3=________;若∠1=40°,则∠3=________;
(3)由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3=________时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC. 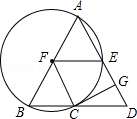
(1)求证:GC是⊙F的切线;
(2)填空: ①若∠BAD=45°,AB=2 ![]() ,则△CDG的面积为 .
,则△CDG的面积为 .
②当∠GCD的度数为时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,边AO在y轴上,点B1 , B2 , B3 , …都在直线y= ![]() x上,则A2017的坐标为( )
x上,则A2017的坐标为( )
A.2015 ![]() ,2017
,2017
B.2016 ![]() ,2018
,2018
C.2017 ![]() ,2019
,2019
D.2017 ![]() ,2017
,2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型手机和2部乙型手机,共需要资金4600元.
(1) 求甲、乙型号手机每部进价为多少元?
(2) 为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
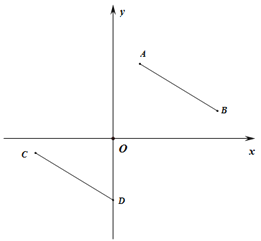
【题目】已知,在平面直角坐标系中,A(1,a)、B(b,1),其中a、b满足![]() +(a+b-7)2=0.
+(a+b-7)2=0.
(1) 求a、b的值;
(2) 平移线段AB至CD,其中A、B的对应点分别为C、D,若D的坐标为(0,n)且n<0,若四边形ABDC的面积为20,求D的坐标;
(3)在(2)的条件下,将线段AB绕点A以每秒80的速度顺时针旋转,同时线段CD绕点D以每秒20的速度顺时针旋转(当AB旋转到一周时两线段同时停止旋转),设运动时间为t秒,当t为何值时,直线AB与直线CD的夹角为600?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
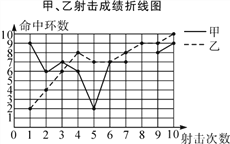
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为条件,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
条件(已知):
结论(求证):
证明:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com