
【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

【答案】![]() .
.
【解析】试题分析:根据已知首先表示出围成的三角形面积为S,得出b=2S ,即D点坐标为(0,2S),再将C、D点坐标代入直线L2的解析式,解出即可.
试题解析:∵直线L1过点A(0,2),B(2,0),直线L2:y=mx+b过点C(1,0)且
把△AOB分成两部分中靠近原点的那部分是一个三角形,
∴可以推出直线L2过第一、二、四象限,
所以可以设直线L2交y轴与D点(0,b),
∵围成的三角形面积为S,根据三角形面积公式可得,
S=![]() ,
,
则b=2S ,也即D点坐标为(0,2S),
将C、D点坐标代入直线L2的解析式,可解出,m=-2S,
∴S关于m的函数解析式为:S=-![]() ,
,
∵S>0且S小于△AOB面积的一半,所以0<S≤1,
∴0<--![]() ≤1,
≤1,
∴-2≤m<0,
∴自变量m的取值范围是:-2≤m<0,
∴S关于m的函数解析式为:S=-![]() (-2≤m<0).
(-2≤m<0).


科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | |
| | 2 | | 4 | | 2 | |
| m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= ![]() 的一条性质: .
的一条性质: .
(5)如果方程 ![]() =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN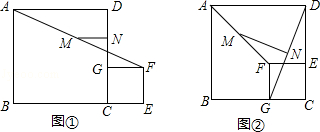
(1)线段MN和GD的数量关系是 , 位置关系是;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )
A.m< ![]()
B.m> ![]() 且m≠2
且m≠2
C.m≤ ![]()
D.m≥ ![]() 且m≠2
且m≠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,……如此继续运动下去.设Pn(xn,yn),n=1、2、3、……,则x1+x2+……+x2014+x2015的值为( )

A. 1 B. 3 C. -1 D. 2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)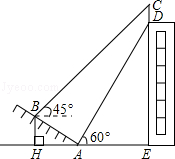
(1)求点B距水平而AE的高度BH;
(2)求宣传牌CD的高度.
(结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=90°,AB=AC , BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第张.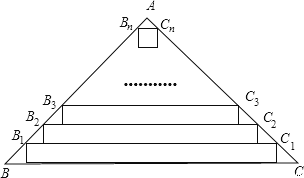
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com