
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

【答案】(1)证明见解析(2)![]() ;(3)
;(3)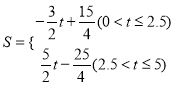 ; (4)
; (4)![]() .
.
【解析】试题分析:(1)根据全等三角形的判定和性质即可得到结论;
(2)根据勾股定理即可得到结论;
(3)由△BCM≌△DCM计算出BM=DM,分两种情况计算即可;
(4)由菱形的性质判断出△ADM≌△ABM,再判断出△BMP是等腰三角形,即可得出结论.
试题解析:解:(1)∵AC是菱形ABCD的对角线,∴∠ACD=∠ACB,CD=CB.在△DCM和△BCM中,∵CD=CB,∠DCM=∠BCM,CM=CM,∴△DCM≌△BCM,∴DM=BM;
(2)在Rt△ADH中,AD=5,AH=3,∴DH=4.在Rt△BHM中,BM=DM,HM=DH﹣DM=4﹣DM,BH=AB﹣AH=2,根据勾股定理得:DM2﹣MH2=BH2,即:DM2﹣(4﹣DM)2=4,∴DM=![]() ,∴MH=
,∴MH=![]() ;
;
(3)在△BCM和△DCM中,∵CM=CN,∠ACD=∠ACB,CB=CD,∴△BCM≌△DCM,∴BM=DM=![]() ,∠CDM=∠CBM=90°.
,∠CDM=∠CBM=90°.
①当P在AB之间时,即0<t<2.5时,S=![]() (5﹣2t)×
(5﹣2t)×![]() =﹣
=﹣![]() t+
t+![]() ;
;
②当P在BC之间时,即2.5<t≤5时,S=![]() (2t﹣5)×
(2t﹣5)×![]() =
=![]() t﹣
t﹣![]() ;
;
综上所述: 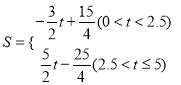 ;
;
(4)存在.∵∠ADM+∠BAD=90°,∠BCD=∠BAD,∴∠ADM+∠BCD=90°.∵∠MPB+∠BCD=90°,∴∠MPB=∠ADM.∵四边形ABCD是菱形,∴∠DAM=∠BAM.∵AM=AM,∴△ADM≌△ABM,∴∠ADM=∠ABM,∴∠MPB=∠ABM.∴MP=MB.∵MH⊥AB,∴PH=BH=2,∴BP=2BH=4.∵AB=5,∴AP=1,∴t=![]() =
=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示. 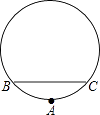
(1)请你帮他们求出该湖的半径;
(2)如果在圆周上再另取一点P,建造一座连接B,C,P三点的三角形艺术桥,且△BCP为直角三角形,问:这样的P点可以有几处?如何找到?
查看答案和解析>>
科目:初中数学 来源: 题型:
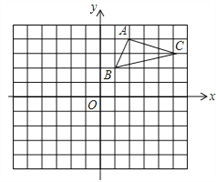
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标A1 ________________.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2__________________.
(3) △ABC是否为直角三角形?答_________(填是或者不是).
(4)利用格点图,画出BC边上的高AD,并求出AD的长,AD=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )

A. ①②④ B. ①③ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′. 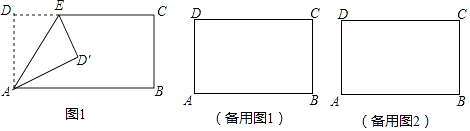
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则PEF和PGH的面积和等于.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com