
【题目】已知ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )

A. ①②④ B. ①③ C. ②③④ D. ①②③④
【答案】D
【解析】因为F是BC的中点,所以F=FC,然后根据平行四边形的性质和AD=2AB,可得到BC=2AB=2CD,即BF=FC=AB,再根据“等边对等角”可得∠AFB=∠BAF,然后平行线的性质,可得∠AFB=∠FAB,即可得到2∠BAF=∠BAD,故①正确;
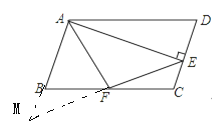
延长EF,交AB的延长线于M,由平行四边形的性质和中点的性质,可证明△MBF≌△ECF(ASA)然后根据全等三角形的性质和垂直的性质证得EF=AF,故②正确;
根据EF=FM可知S△EFC=S△AFM,所以可得S△ABF≤S△AEF,故③正确;
设∠FEA=x,则∠FAE=x,可得∠BAF=∠AFB=90°-x,进而求得∠EFA=180°-2x,则∠EFB=90°-x+180°-2x=270°-3x,再根据∠CFE=90°-x,可得∠BFE=3∠CEF,故④正确.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料并填空: 在体育比赛中,我们常常会遇到计算比赛场次的问题,这时我们可以借助数线段的方法来计算.比如在一个小组中有 4 个队,进行单循环比赛,我们要计算总的比赛场次,我们就 设这四个队分别为 A、B、C、D,并把它们标在同一条线段上,如下图:
![]()
因为单循环比赛就是每两个队之间都要比赛一场,这就相当于,在上述图形中四个点连接线段,按一定规律得到的线段有:
AB,AC,AD…………3 条
BC,BD………………2 条
CD……………………1 条
总的线段条数是 3+2+1=6
所以可知 4 个队进行单循环比赛共比赛六场.
(1).类比上述想法,若一个小组有 6 个队,进行单循环比赛,则总的比赛场次是_____
(2).类比上述想法,若一个小组有 n 个队,进行单循环比赛,则总的比赛场次是_____
(3).我们知道 2006 年世界杯共有 32 支代表队参加比赛,共分成 8 个小组,每组 4 个 代表队.第一阶段每个小组进行单循环比赛.则第一阶段共 需 要 进 行_______ 场比赛.
(4).若分成 m 个小组,每个小组有 n 个队,第一阶段每个小组进行单循环比赛.则第 一阶段共需要进行_____________场比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生“自主学习、合作交流”的情况,对八年级各班部分同学进行了一段时间的跟踪调査,将调查结果(A:特别好; B:较好; C:一般; D:较差)绘制成以下两幅不完整的统计图. 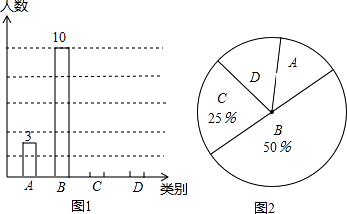
请根据图中提供的信息,解答下列问题:
(1)此次跟踪调查的学生有人;扇形统计图中,D类所占圆心角为度;
(2)补全条形统计图;
(3)如果该校八年级共有学生360人,试估计A类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com