
【题目】阅读下列材料并填空: 在体育比赛中,我们常常会遇到计算比赛场次的问题,这时我们可以借助数线段的方法来计算.比如在一个小组中有 4 个队,进行单循环比赛,我们要计算总的比赛场次,我们就 设这四个队分别为 A、B、C、D,并把它们标在同一条线段上,如下图:
![]()
因为单循环比赛就是每两个队之间都要比赛一场,这就相当于,在上述图形中四个点连接线段,按一定规律得到的线段有:
AB,AC,AD…………3 条
BC,BD………………2 条
CD……………………1 条
总的线段条数是 3+2+1=6
所以可知 4 个队进行单循环比赛共比赛六场.
(1).类比上述想法,若一个小组有 6 个队,进行单循环比赛,则总的比赛场次是_____
(2).类比上述想法,若一个小组有 n 个队,进行单循环比赛,则总的比赛场次是_____
(3).我们知道 2006 年世界杯共有 32 支代表队参加比赛,共分成 8 个小组,每组 4 个 代表队.第一阶段每个小组进行单循环比赛.则第一阶段共 需 要 进 行_______ 场比赛.
(4).若分成 m 个小组,每个小组有 n 个队,第一阶段每个小组进行单循环比赛.则第 一阶段共需要进行_____________场比赛.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,□ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
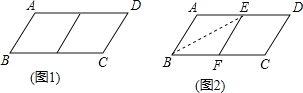
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行如下操作:如图2,把□ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABEF是菱形.
(2)操作、探究与计算:
①已知□ABCD是邻边长分别为1,a(a>1),且是3阶准菱形,请画出□ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知□ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r(r>0),则□ABCD
是 阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=![]() ,那么AC的长等于__________ .
,那么AC的长等于__________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 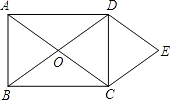
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )

A. ①②④ B. ①③ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com