
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 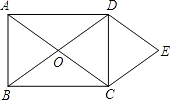
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
【答案】
(1)解:四边形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形
(2)解:连接OE.由菱形OCED得:CD⊥OE,
又∵BC⊥CD,
∴OE∥BC(在同一平面内,垂直于同一条直线的两直线平行),
又∵CE∥BD,
∴四边形BCEO是平行四边形;
∴OE=BC=8(7分)
∴S四边形OCED= ![]() OECD=
OECD= ![]() ×8×6=24.
×8×6=24.

【解析】(1)首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.(2)连接OE,通过证四边形BOEC是平行四边形,得OE=BC;根据菱形的面积是对角线乘积的一半,可求得四边形ODEC的面积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位) 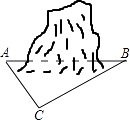
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并填空: 在体育比赛中,我们常常会遇到计算比赛场次的问题,这时我们可以借助数线段的方法来计算.比如在一个小组中有 4 个队,进行单循环比赛,我们要计算总的比赛场次,我们就 设这四个队分别为 A、B、C、D,并把它们标在同一条线段上,如下图:
![]()
因为单循环比赛就是每两个队之间都要比赛一场,这就相当于,在上述图形中四个点连接线段,按一定规律得到的线段有:
AB,AC,AD…………3 条
BC,BD………………2 条
CD……………………1 条
总的线段条数是 3+2+1=6
所以可知 4 个队进行单循环比赛共比赛六场.
(1).类比上述想法,若一个小组有 6 个队,进行单循环比赛,则总的比赛场次是_____
(2).类比上述想法,若一个小组有 n 个队,进行单循环比赛,则总的比赛场次是_____
(3).我们知道 2006 年世界杯共有 32 支代表队参加比赛,共分成 8 个小组,每组 4 个 代表队.第一阶段每个小组进行单循环比赛.则第一阶段共 需 要 进 行_______ 场比赛.
(4).若分成 m 个小组,每个小组有 n 个队,第一阶段每个小组进行单循环比赛.则第 一阶段共需要进行_____________场比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB∥CD,∠A=∠C;③AO=CO,BO=DO;④AB∥CD,AD=BC.
一定能判定四边形ABCD是平行四边形的条件有----------------------------( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生“自主学习、合作交流”的情况,对八年级各班部分同学进行了一段时间的跟踪调査,将调查结果(A:特别好; B:较好; C:一般; D:较差)绘制成以下两幅不完整的统计图. 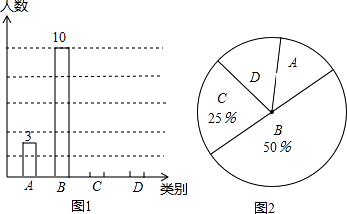
请根据图中提供的信息,解答下列问题:
(1)此次跟踪调查的学生有人;扇形统计图中,D类所占圆心角为度;
(2)补全条形统计图;
(3)如果该校八年级共有学生360人,试估计A类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com