
【题目】四边形ABCD中,对角线AC、BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB∥CD,∠A=∠C;③AO=CO,BO=DO;④AB∥CD,AD=BC.
一定能判定四边形ABCD是平行四边形的条件有----------------------------( )
A. 1组 B. 2组 C. 3组 D. 4组
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 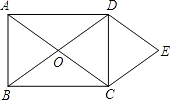
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
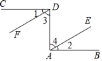
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的顶点A在原点O处,点B在x轴上,点C的坐标为(6,6),点D在y轴上,动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度. 
(1)探索AQ与BP有什么样的关系?并说明理由;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,求线段CE的长.
(3)如图3,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,∠BAC=60°,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是点D、E.
(1)如图1,当点D恰好落在边AB上时,试判断DE与AC的位置关系,并说明理由.
(2)如图2,当点B、D、E三点恰好在一直线上时,旋转角α=__°,此时直线CE与AB的位置关系是__.
(3)在(2)的条件下,联结AE,设△BDC的面积S1,△AEC的面积S2,则S1与S2的数量关系是_____.
(4)如图3,当点B、D、E三点不在一直线上时,(3)中的S1与S2的数量关系仍然成立吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )

A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com