
【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′. 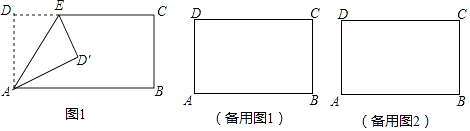
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长.
【答案】
(1)解:如图1,在Rt△ABC中,
∵∴AD′=AD=5,
∵AC= ![]() =
= ![]() =
= ![]() ,
,
∴CD′=AC﹣AD′= ![]() ﹣5
﹣5
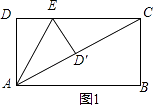
(2)解:①当D′落在对称轴GH上,
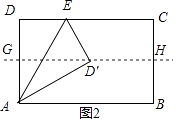
∵GH是矩形对称轴,
∴AC= ![]() AD,
AD,
由翻折的性质得:AD′=AD,∠DAE= ![]() ∠DAD′,
∠DAD′,
∴GA= ![]() AD′,
AD′,
∴在Rt△AGD′中,∠GAD′=60°,
∴∠DAE= ![]() ∠DAD′=30°,
∠DAD′=30°,
在Rt△ADE中,
∵tan∠DAE= ![]() ,即:tan30°=
,即:tan30°= ![]() ,
,
∴DE= ![]() ,
,
②当D′落在对称轴MN上,又分两种情况,
第一种:点E在DC上,如图3,
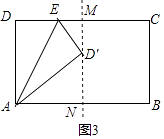
∵MN是矩形对称轴,
∴DM=AN=4,
由翻折得:AD′=AD,
在Rt△AND′中,
D′N= ![]() =3,
=3,
∴D′M=MN﹣D′N=5﹣3=2,
设DE=ED′=x,
在Rt△EAD′中,
ED′2=EM2+MD′2,
即:x2=(4﹣x)2+22,
解之得:x= ![]() ,即DE=
,即DE= ![]() ,
,
第二种:点E在DC延长线上,如图4,方法同上,DE=10.

综上所述,点D′落在矩形对称轴上时,DE的长为 ![]() 或
或 ![]() 或10.
或10.
【解析】(1)如图1,在Rt△ABC中,根据勾股定理即可得到结论;(2)①当D′落在对称轴GH上,由翻折的性质得到AD′=AD,∠DAE= ![]() ∠DAD′,求得GA=
∠DAD′,求得GA= ![]() AD′,根据三角形的内角和得到∠DAE=
AD′,根据三角形的内角和得到∠DAE= ![]() ∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N=
∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N= ![]() =3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE=
=3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE= ![]() ,第二种:点E在DC延长线上,同理得到结论.
,第二种:点E在DC延长线上,同理得到结论.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早 ![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题: 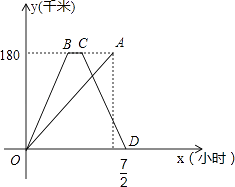
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置某种教学仪器,现有两种添置方法.方案1:到厂商家购买,每件需要8元和一次性的运费2000元;方案2:学校自己制作,每件4元,另外购置制作工具的费用4200元.现所需教学仪器件数不明确.
请你给校长出出主意,选择哪种方案更节约费用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=-![]() ,y=-2.甲同学把“x=-
,y=-2.甲同学把“x=-![]() ”错抄成“x=
”错抄成“x=![]() ”.但他计算的结果是正确的,请你分析这是什么原因.
”.但他计算的结果是正确的,请你分析这是什么原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法: ①abc<0;
②2a﹣b=0;
③4a+2b+c<0;
④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 .
,y2)是抛物线上两点,则y1>y2 .
其中说法正确的是( )
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策:安装”一户一表”的居民
用户,按用抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,其中低于50千瓦时(含50
千瓦时)部分电价不调整;51—200千瓦时部分每千瓦时电价上调0.03元;超过200千瓦时部分每千
瓦时电价上调0.10元.已知调整前电价统一为每千瓦时0.53元.
(1)若许老师家10月份的用电量为130千瓦时,则10月份许老师家应付电费多少元?
(2)已知许老师家10月份的用电量为![]() 千瓦时,请完成下列填空:
千瓦时,请完成下列填空:
①若![]() 千瓦时,则10月份许老师家应付电费为 元;
千瓦时,则10月份许老师家应付电费为 元;
②若50<![]() ≤200千瓦时,则10月份许老师家应付电费为 元;
≤200千瓦时,则10月份许老师家应付电费为 元;
③若![]() >200千瓦时,则10月份许老师家应付电费为 元.
>200千瓦时,则10月份许老师家应付电费为 元.
(3)若10月份许老师家应付电费为96.50元,则10月份许老师家的用电量是多少千瓦时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com