
 ��֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=-$\frac{3}{4}$x+6��x�ᡢy��Ľ���ֱ�ΪA��B���㣬����OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C��
��֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=-$\frac{3}{4}$x+6��x�ᡢy��Ľ���ֱ�ΪA��B���㣬����OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C������ ��1��������Գƺͽ�ƽ���ߵ������Լ����ɶ����������OC�ij��ȣ��Ӷ������C�����꣮�ٸ���ֱ�ߵĽ���ʽ���A��B�����꣬������ô���ϵ�����Ϳ�����������ߵĽ���ʽ��
��2�����ݣ�1���Ľ���ʽ����ת��Ϊ����ʽ�������������D������B��C���������BC�Ľ���ʽ��������ֱ��BC�ϴ������������ĵ�P������ƽ���ı��ε����ʺ�������ȫ�ȵ����������P�����꣬�õ���P����ֱ��BC�ϣ����ó����ۣ�
��3��ƽ�ƺ���ݣ�1���Ľ���ʽ���Եõ�ƽ�ƺ�Ľ���ʽ���������꼰�Գ��ᣬ���������������Ľ���F��N��E�����꣬����EF������E��F��������������ʽ�����EF��Գ���Ľ��㣬����Q�㣮
��� 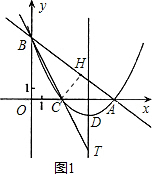 �⣺��1������CH��
�⣺��1������CH��
����ԳƵ�CH��AB��BH=BO��CH=CO
���ڡ�CHA���ɹ��ɶ�������
AC2=CH2+AH2
��ֱ��y=$\frac{3}{4}$x+6��x�ᡢy��Ľ���ֱ�ΪA��B���㣬
�൱x=0ʱ��y=6����y=0ʱ��x=8
��B��0��6����A��8��0��
��OB=6��OA=8��
��Rt��AOB�У��ɹ��ɶ�������
AB=10
��C��a��0������OC=a
��CH=a��AH=4��AC=8-a����Rt��AHC��
�ɹ��ɶ�������
��8-a��2=a2+42���
a=3
C��3��0��
�������ߵĽ���ʽΪ��y=ax2+bx+c�������⣬��
$\left\{\begin{array}{l}{6=c}\\{0=64a+8b+c}\\{0=9a+3b+c}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-\frac{11}{4}}\\{c=6}\end{array}\right.$
�������ߵĽ���ʽΪ��y=$\frac{1}{4}$x2$-\frac{11}{4}x$+6��
��y=$\frac{1}{4}$${��x-\frac{11}{2}��}^{2}$$-\frac{25}{16}$��
��2���ɣ�1���Ľ��ۣ���
D��$\frac{11}{2}$��-$\frac{25}{16}$��
��DF=$\frac{25}{16}$��
��BC�Ľ���ʽΪ��y=kx+b������
$\left\{\begin{array}{l}{6=b}\\{0=3k+b}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{b=6}\\{k=-2}\end{array}\right.$
ֱ��BC�Ľ���ʽΪ��y=-2x+6
����ڵ�Pʹ�ı���ODAP��ƽ���ı��Σ�P��m��n��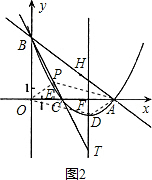
��PE��OA��E��HD��OA��F��
���PEO=��AFD=90�㣬PO=DA��PO��DA
���POE=��DAF
���OPE�ա�ADF
��PE=DF=n=$\frac{25}{16}$��
��$\frac{25}{16}$=-2x+6
��$x=\frac{71}{32}$
P��$\frac{5}{2}$��$\frac{25}{16}$��
��x=$\frac{5}{2}$ʱ��
y=-2��$\frac{5}{2}$+6=1��$\frac{25}{16}$
���P����ֱ��BC�ϣ���ֱ��BC�ϲ��������������ĵ�P��
��3��������ã�ƽ�ƺ�Ľ���ʽΪ��
y=$\frac{1}{4}$��x-2��2$-\frac{25}{16}$
��Գ���Ϊ��x=2��
��x=0ʱ��y=-$\frac{9}{16}$
��y=0ʱ��0=$\frac{1}{4}$��x-2��2$-\frac{25}{16}$
��ã�x1=$-\frac{1}{2}$��x2=$\frac{9}{2}$
��F��N�����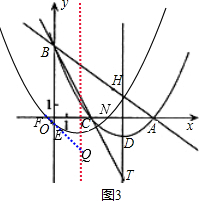
F��$-\frac{1}{2}$��0����E��0��-$\frac{9}{16}$����N��$\frac{9}{2}$��0��
����EF��x=2��Q����EF�Ľ���ʽΪ��y=kx+b������
$\left\{\begin{array}{l}{0=-\frac{1}{2}k+b}\\{b=-\frac{9}{16}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{k=-\frac{9}{8}}\\{b=-\frac{9}{16}}\end{array}\right.$
��EF�Ľ���ʽΪ��y=-$\frac{9}{8}$x-$\frac{9}{16}$
��$\left\{\begin{array}{l}{y=-\frac{9}{8}x-\frac{9}{16}}\\{x=2}\end{array}\right.$
��ã�
$\left\{\begin{array}{l}{x=2}\\{y=-\frac{45}{16}}\end{array}\right.$
��Q��2��-$\frac{45}{16}$����
���� ������һ�����κ������ۺ����⣬��������ԳƵ����ʣ����ɶ��������ã�����ϵ���������Ľ���ʽ�ķ�����ͼ���ƽ�ƣ�ƽ���ı��ε��ж��������Լ���ֵ��ȷ���ȶ��֪ʶ�㣬�ۺ����ö��κ��������ʼ�ƽ���ı��ε����ʣ�������������ǽ�����Ĺؼ���


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����Խ����ഹֱƽ�ֵ��ı����Ǿ��� | |
| B�� | ��һ���Խ���ƽ��һ��Խǵ��ı��������� | |
| C�� | �����Խ�����ȵ��ı����Ǿ��� | |
| D�� | һ��Ա�ƽ�У�һ��Խ���ȵ��ı�����ƽ���ı��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AD�ǡ�ABC�С�BAC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��S��ABC=7��DE=2��AB=4����AC���ǣ�������
��ͼ��AD�ǡ�ABC�С�BAC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��S��ABC=7��DE=2��AB=4����AC���ǣ�������| A�� | 3 | B�� | 4 | C�� | 6 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=2 | B�� | x=-2 | C�� | x=1 | D�� | x=-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
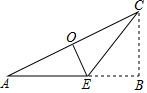 ��ͼ����Rt��ABC�У���E��AB�ϣ������ֱ����������CE�۵���ʹ��Bǡ���䵽б��AC���е�O������BC=3�����ۺ�CE�ij�Ϊ��������
��ͼ����Rt��ABC�У���E��AB�ϣ������ֱ����������CE�۵���ʹ��Bǡ���䵽б��AC���е�O������BC=3�����ۺ�CE�ij�Ϊ��������| A�� | $\sqrt{3}$ | B�� | 2$\sqrt{3}$ | C�� | 3$\sqrt{3}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
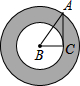 ��ͼ����Rt��ABC�У���C=90�㣬������B��˳ʱ����תһ�ܣ���ֱ���BA��BCΪ�뾶��Բ���γ�һԲ������Ӱ���֣���Ϊ���Բ���������ֻ�����һ���߶εij��ȣ������߶ξ��ǣ�������
��ͼ����Rt��ABC�У���C=90�㣬������B��˳ʱ����תһ�ܣ���ֱ���BA��BCΪ�뾶��Բ���γ�һԲ������Ӱ���֣���Ϊ���Բ���������ֻ�����һ���߶εij��ȣ������߶ξ��ǣ�������| A�� | AD | B�� | AB | C�� | BD | D�� | AC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com