Question

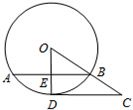
如图, CD切⊙O于点D,连结OC, 交⊙O于点B,过点B作弦AB⊥OD，点E为垂足,已知⊙O的半径为10,sin∠COD=.

求：（1）弦AB的长；

（2）CD的长；

（3）劣弧AB的长（结果保留三个有效数字, sin53.13^o ≈0.8, ≈3.142）.

Answer 1

解：(1)∵ AB⊥OD，

∴∠OEB=90⁰

在Rt△OEB中，BE=OB×sin∠COD=10×=8

由垂径定理得AB=2BE=16

所以弦AB的长是16   

(2)方法（一）

在Rt△OEB中，   OE= =6.

∵CD切⊙O于点D,    ∴∠ODC=90⁰, ∴∠OEB=∠ODC.

∵∠BOE=∠COD,   ∴△BOE∽△COD,

∴ ,   ∴ ,     ∴CD= .

所以CD的长是                       

方法（二）由sin∠COD= 可得tan∠COD= ,

在Rt△ODC中，tan∠COD= ,

∴CD=OD•tan∠COD=10×=                

(3)连结OA. 在Rt△ODC中， ∵sin53.13^o ≈0.8    ∴∠DOC=53.13^o

∴∠AOB=106.26^o ，

∴劣弧AB的长度 ≈18.5