
【题目】如图,已知在△ABC中,AB=AC,以AB为直径的半圆O与边BC交于点D,与边AC交于点E,过点D作DF⊥AC于F.
(1)求证:DF为⊙O的切线;(2)若DE=![]() ,AB=
,AB=![]() ,求AE的长.
,求AE的长.

【答案】(1)证明见解析;(2)![]()
【解析】(1)连接AD、CD,则∠ADB=90°,AD⊥BC,又因为AB=AC,所以BD=DC,OA=OB,OD∥AC,易证DF⊥OD,故DF为⊙O的切线;
(2)连接BE交OD于G,由于AC=AB,AD⊥BC,ED⊥BD,故∠EAD=∠BAD, ![]() =
=![]() ,ED=BD,OE=OB,
,ED=BD,OE=OB,
故OD垂直平分EB,EG=BG,因为AO=BO,所以OG=![]() AE,在Rt△DGB和Rt△OGB中,BD2-DG2=BO2-OG2,代入数值即可求出AE的值.
AE,在Rt△DGB和Rt△OGB中,BD2-DG2=BO2-OG2,代入数值即可求出AE的值.
证明:(1)连接AD,OD,∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=DC,∵OA=OB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∴DF为⊙O的切线;

(2)连接BE交OD于G,∵AC=AB,AD⊥BCED⊥BD,∴∠EAD=∠BAD,∴![]() ,∴ED=BD,OE=OB,∴OD垂直平分EB,∴EG=BG,又AO=BO,
,∴ED=BD,OE=OB,∴OD垂直平分EB,∴EG=BG,又AO=BO,
∴OG=![]() AE.在Rt△DGB和Rt△OGB中,
AE.在Rt△DGB和Rt△OGB中,
BD2﹣DG2=BO2﹣OG2,∴(![]() )2-(
)2-(![]() -OG)2=BO2-OG2,
-OG)2=BO2-OG2,
解得:OG=![]() .∴AE=2OG=
.∴AE=2OG=![]() .
.
“点睛”本题比较复杂,涉及到切线的判定定理及勾股定理,等腰三角形的性质,具有很强的综合性.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①DF=DN;③AE=CN;③△DMN是等腰三角形;④∠BMD=45°,其中正确的结论个数是( ) 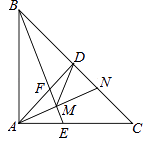
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有数字-1、-2、1、2.从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字可能出现的所有结果;
(2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数字都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3. ![]()
(1)若CE=8,求AC的长;
(2)若C是AB的中点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a. 如:1⊕3=1×32+2×1×3+1=16.
(1)求(﹣2)⊕3的值;
(2)若( ![]() ⊕3)⊕(﹣
⊕3)⊕(﹣ ![]() )=8,求a的值.
)=8,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com