
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.

【答案】(1)①见解析②∠BOA=2α(2)见解析
【解析】
(1)①根据等腰三角形的性质和三角形的内角和得到∠ACB=∠DCE,根据全等三角形的性质即可得到结论;
②根据全等三角形的性质得到∠CAD=∠CBE=α+∠BAO,根据三角形的内角和即可得到结论;
(2)如图2,作BP⊥MN的延长线上于点P,作DQ⊥MN于Q,根据全等三角形的性质得到MC=BP,同理CM=DQ,等量替换得到DQ=BP,根据全等三角形的性质即可得到结论.
(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°-2α,∠DCE=180°-2α,
∴∠ACB=∠DCE
∴∠ACB-∠DCB=∠DCE-∠DCB
∴∠ACD=∠BCE
在△ACD和△BCE中
∴△ACD≌△BCE
∴BE=AD;
②∵△ACD≌△BCE
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO
∴∠CBE+α=∠BOA+∠BAO
∴∠BAO+α+α=∠BOA+∠BAO
∴∠BOA=2α
(2)如图2,作BP⊥MN的延长线上于点P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC
∴∠BCA=∠AMC
∴∠BCP=∠CAM
在△CBP和△ACM中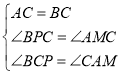
∴△CBP≌△ACM(AAS)
∴MC=BP.
同理△CDQ≌△ECM
∴CM=DQ
∴DQ=BP
在△BPN和△DQN中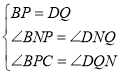
∴△BPN≌△DQN
∴BN=ND,
∴N是BD中点.



 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强建设“经济强、环境美、后劲足、群众富”的实力城镇,聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶计划。现决定将A、B两种类型鱼苗共320箱运到某村养殖,其中A种鱼苗比B种鱼苗多80箱。
(1)求A种鱼苗和B种鱼苗各多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱,乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元,则安排甲、乙两种货车有哪几种不同的方案?并说明选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,∠ABC+∠ADC=180,连接AC,BD.
(1)如图1,当∠ACD=∠CAD=45时,求∠CBD的度数;
(2)如图2,当∠ACD=∠CAD=60时,求证:AB+BC=BD;
(3)如图3,在(2)的条件下,过点C作CK⊥BD于点K,在AB的延长线上取点F,使∠FCG=60,过点F作FH⊥BD于点H,BD=8,AB=5,GK=![]() ,求BH的长。
,求BH的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.

(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
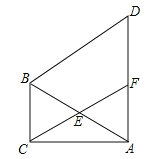
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的门票销售分两类:一类为散客门票,价格为![]() 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票![]() 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打![]() 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游![]() 人,购买门票需要
人,购买门票需要![]() 元
元
(1)如果每人分别买票,求![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:
(2)如果购买团体票,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(3)请根据人数变化设计一种比较省钱的购票方式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com