
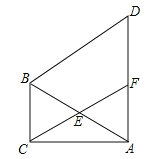
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
【答案】(1)证明见解析;(2)9![]() .
.
【解析】
(1)在Rt△ABC 中,E为AB的中点,则CE![]() AB,BE
AB,BE![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°,又∠D=60°,得∠AFE=∠D=60°,所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,由此即可得四边形BCFD是平行四边形;
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°,又∠D=60°,得∠AFE=∠D=60°,所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,由此即可得四边形BCFD是平行四边形;
(2)在Rt△ABC中,求出BC,AC即可解决问题.
(1)在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,
∵E为AB的中点,∴AE=BE,
又∵∠AEF=∠BEC,∴△AEF≌△BEC,
在△ABC中,∠ACB=90°,E为AB的中点,
∴CE![]() AB,BE
AB,BE![]() AB,
AB,
∴CE=AE,
∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,
又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,
∴四边形BCFD是平行四边形;
(2)在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC![]() AB=3,AC=
AB=3,AC=![]() =3
=3![]() ,
,
∴S平行四边形BCFD=3![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 . 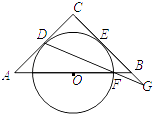
查看答案和解析>>
科目:初中数学 来源: 题型:
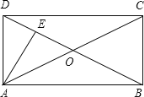
【题目】如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数( )
A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )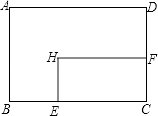
A.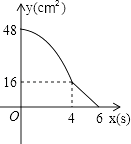
B.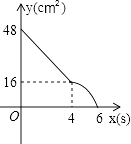
C.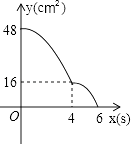
D.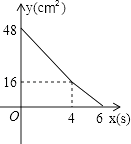
查看答案和解析>>
科目:初中数学 来源: 题型:
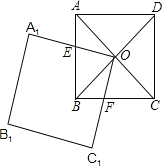
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,O又是正方形A1B1C1O的一个顶点,OA1交AB于点E,OC1交BC于点F.
(1)求证:△AOE≌△BOF;
(2)如果两个正方形的边长都为a,那么正方形A1B1C1O绕O点转动,两个正方形重叠部分的面积等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: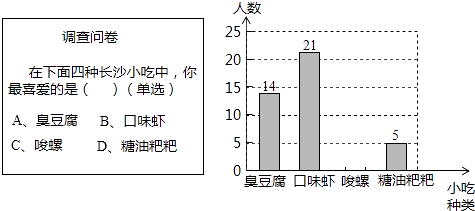
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com