
����Ŀ��ij��ѧ��ȤС����ȫУ��Χ�������ȡ��50��ͬѧ���С�����ϵij�ɳ������ϲ���ij�ɳС�ԡ��������������ʾ���������Ƴ���ͼ��ʾ�IJ���������ͳ��ͼ��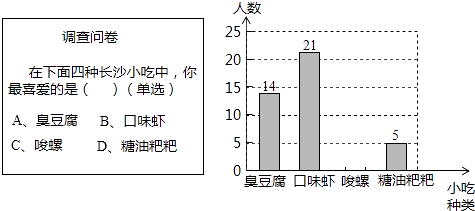
�����������Ϣ����������⣺
��1���벹ȫ����ͳ��ͼ��
��2����ȫУ��2000��ͬѧ�������ȫУͬѧ����ϲ��������������ͬѧ�ж����ˣ�
��3����һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ����С�Ե����A��B��C��D�����������һ��С��Ȼ��Żأ������������һ��С�������б�������ͼ�ķ��������ǡ�����ζ�������A���ĸ��ʣ�
���𰸡�
��1���⣺��������ã�ϲ�������ݡ�����Ϊ��50����14+21+5��=10���ˣ���
��ȫͳ��ͼ����ͼ��ʾ��
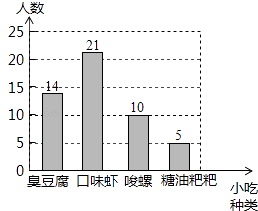
��2���⣺��������ã�2000�� ![]() ��100%=560���ˣ���
��100%=560���ˣ���
�����ȫУͬѧ����ϲ��������������ͬѧ��560�ˣ�
��3���⣺�б����£�
A | B | C | D | |
A | ��A��A�� | ��B��A�� | ��C��A�� | ��D��A�� |
B | ��A��B�� | ��B��B�� | ��C��B�� | ��D��B�� |
C | ��A��C�� | ��B��C�� | ��C��C�� | ��D��C�� |
D | ��A��D�� | ��B��D�� | ��C��D�� | ��D��D�� |
���еȿ��ܵ������16�֣�����ǡ�����ζ�������A���������1�֣�
��P= ![]() ��
��
����������1���������������ڸ�����Ƶ��֮�Ϳ����ϲ�������ݡ���������Ȼ��ȫ����ͳ��ͼ���ɣ�
��2�����ݰٷֱ�=Ƶ�����������ϲ�������������İٷֱȣ�Ȼ����2000������ٷֱȼ��ɣ�
��3�������б��ó����еȿ��ܵ���������ҳ�ǡ�����ζ�������A�������������������ø��ʹ�ʽ���м��㼴��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
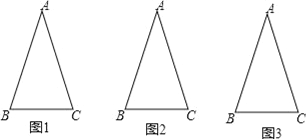
����Ŀ����ͼ����ABC�У�AB=AC����A=36�����������������������Ϊ�ƽ���������Σ���������²���������ͼ��Ҫ��ʹ��Բ�棬����������ָ�ĵ��������θ�������������ABC��
��1����ͼ1�л�1���߶Σ�ʹͼ����2�����������Σ���ֱ��д����2�����������εĶ��Ƕ����ֱ����������������Ⱥ��������������ȣ�
��2����ͼ2�л�2���߶Σ�ʹͼ����4�����������Σ�
��3�����������ϲ������֣�����ABC�л�n���߶Σ���ͼ���������������������������Σ����������������������ƽ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
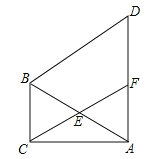
����Ŀ����ͼ���ڡ�ABC������ACB��90�㣬��CAB��30�㣬���߶�ABΪ���������ȱߡ�ABD����E���߶�AB���е�������CE���ӳ����߶�AD�ڵ�F��
��1����֤���ı���BCFDΪƽ���ı�����
��2����AB��6����ƽ���ı���BCFD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������Ƶ�����ƴͼ��ߵ�һ���֣����������������������⣬��������������֪����ͼ��![]() ��
��
��1����![]() ����
����![]() �Ķ���������գ�
�Ķ���������գ�
��:��1������![]() ��ֱ��
��ֱ��![]() ����ͼ��ʾ����
����ͼ��ʾ����
��Ϊ![]() ����֪����
����֪����
����![]() ��ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ�У���
��ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ�У���
��Ϊ![]() ��
��
![]() �� ����
�� ����
����Ϊ![]() = 60�㣨������������
= 60�㣨������������
����![]() �㣨��ʽ���ʣ�
�㣨��ʽ���ʣ�
��2��ֱ��д����B����D���BFD֮���������ϵ�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���á���������һ�������㣺��������������a��b���涨a��b��ab2+2ab+a��
�磺1��2��1��22+2��1��2+1��9
��1������2����3���� ��
��2����![]() ��3��16����a��ֵ��
��3��16����a��ֵ��
��3����2��x��m����![]() x����3��n������xΪ�����������ԱȽ�m��n�Ĵ�С��
x����3��n������xΪ�����������ԱȽ�m��n�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ���˽���꼶ѧ�����������������������ʦ���꼶(1)��50��ѧ������һ���������������ԣ��Բ�������Ϊ���������Ƴ���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ(��ͼ)��
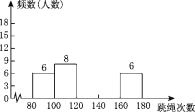
��� | ����(x) | Ƶ��(����) |
��1�� | 80��x��100 | 6 |
��2�� | 100��x��120 | 8 |
��3�� | 120��x��140 | a |
��4�� | 140��x��160 | 18 |
��5�� | 160��x��180 | 6 |
����ͼ������������⣺
(1)���е�a��________��
(2)���Ƶ���ֲ�ֱ��ͼ����������
(3)���涨��x��120Ϊ���ϸ�120��x��140Ϊ�ϸ�140��x��160Ϊ����x��160Ϊ�ţ�����������Ϣ�������ѧУ����꼶ͬѧ��һ�����������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��࣬���ȱ�������ADE��AC��BE�ཻ�ڵ�F�����BFCΪ�� ��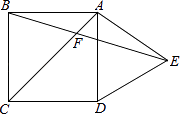
A.75��
B.60��
C.55��
D.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD����һ���߶Σ�����AE�AEF��EF�AFC������AE=6��EF=8��FC=10�����������������Բ֮���γɵ���Ӱ���ֵ����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��A��4��0����B��1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��
��1���������ߵı���ʽ��
��2����P����������һ���㣬��λ�ڵ������ޣ�����ABP�����Ϊ6ʱ�������P�����ꣻ
��3������M��ֱ��BH���˶�����N��x�����˶������Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ����ֱ��д����ʱ��CMN�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com