
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
【答案】
(1)解:把点A(4,0),B(1,3)代入抛物线y=ax2+bx得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线表达式为:y=﹣x2+4x;
(2)解:过P点作PD⊥BH交BH于点D,如图1, 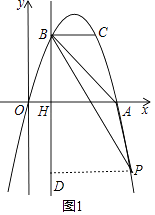
设点P(m,﹣m2+4m),
BH=AH=3,HD=m2﹣4m,PD=m﹣1,
∵S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
![]() ×3×3+
×3×3+ ![]() (3+m﹣1)(m2﹣4m)﹣
(3+m﹣1)(m2﹣4m)﹣ ![]() (m﹣1)(3+m2﹣4m)=6,
(m﹣1)(3+m2﹣4m)=6,
整理得3m2﹣15m=0,解得m1=0(舍去),m2=5,
∴点P坐标为(5,﹣5);
(3)解:∵抛物线的对称性为直线x=2,
而点C、B关于抛物线的对称轴对称,
∴C(3,3),
以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2, 
CM=MN,∠CMN=90°,易证得△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴MC= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
②以点M为直角顶点且M在x轴下方时,如图3, 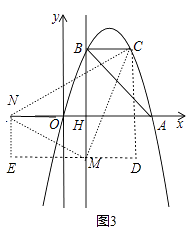
过点M作DE⊥y轴,作NE⊥DE于E,CD⊥DE于D,作辅助线,易得Rt△NEM≌Rt△MDC,
∴MD=NE=BC=2,EM=CD=BM=3+2=5,
∴CM= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
③以点N为直角顶点且N在y轴左侧时,如图4, 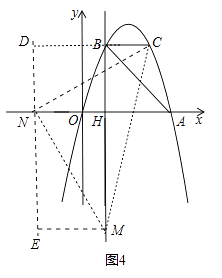
CN=MN,∠MNC=90°,易得Rt△NEM≌Rt△CDN,
∴EM=DN=BH=3,NE=CD=BD+BC=EM+BC=5,
∴CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =17;
=17;
④以点N为直角顶点且N在y轴右侧时,如图5, 
易得Rt△NEM≌Rt△CDN,
∴EM=DN=BH=3,NE=CD=BD﹣BC=EM﹣BC=1,
∴CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =5;
=5;
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上所述:△CMN的面积为: ![]() 或
或 ![]() 或17或5.
或17或5.
【解析】本题是二次函数与几何的综合题目.此题目综合性比较强,解答此题的关键是结合图形做出辅助线.
(1)利用待定系数法求出抛物线的表达式;
(2)过P作PD⊥BH交BH于点D,设P点的坐标为![]() ,则BH=AH=3,HD=m2-4m,PD=m-1,根据S△ABP+S四边形HAPD-S△BPD得到关于m的方程,解方程可得P的坐标;
,则BH=AH=3,HD=m2-4m,PD=m-1,根据S△ABP+S四边形HAPD-S△BPD得到关于m的方程,解方程可得P的坐标;
(3)先利用抛物线的对称性得到C(3,3),下面分五种情况讨论:①以点M在直角顶点且M在x轴上方时;②以点M在直角顶点且M在x轴下方时;③以点N在直角顶点且N在y轴左侧时;④以点N在直角顶点且N在y轴右侧时;⑤以点C在直角顶点时,不能构成满足条件的等腰直角三角形.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: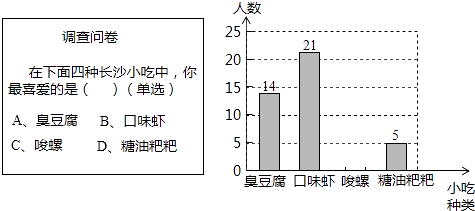
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市2000名年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:

(1)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() ,
,![]() ;
;
(2)请在图中补全频数分布直方图;
(3)如果把成绩在100分以上(含100分)定为优秀,那么该市2000名七年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是AC的中点,B是线段AC上任意一点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )
![]()
A.MN=OCB.MO=![]() (AC-AB)
(AC-AB)
C.ON=![]() (AC - CB)D.MN=
(AC - CB)D.MN=![]() (AC+OB)
(AC+OB)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠ACB的平分线,且交于点O,则图中等腰三角形有________
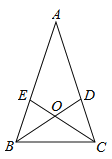
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
路程s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶的路程为20 km时,所花的时间是多少分钟?
(3)随着t逐渐变大,s的变化趋势是什么?
(4)路程s与时间t之间的函数表达式为______________.
(5)按照这一行驶规律,当所花的时间t是300 min时,汽车行驶的路程s是多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com