
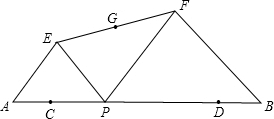
 如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别延长AE、BF交于点H,易证四边形EPFH为平行四边形,得出G为PH中点,则G的运行轨迹为三角形HCD的中位线MN.再求出CD的长,运用中位线的性质求出MN的长度即可确定③正确;又由G为EF的中点,∠EPF=90°,可知②错误.根据直角三角形两直角边的差越大,直角三角形的面积越小,可求得答案.
解答 解:如图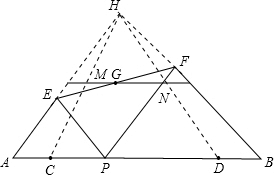 ,
,
分别延长AE、BF交于点H.
∵等腰Rt△APE和等腰Rt△PBF,
∴∠A=∠FPB=45°,∠B=∠EPA=45°,
∴AH∥PF,BH∥PE,∠EPF=180°-∠EPA-∠FPB=90°,
∴四边形EPFH为平行四边形,
∴EF与HP互相平分.
∵G为EF的中点,
∴G也为PH中点,
即在P的运动过程中,G始终为PH的中点,
∴G的运行轨迹为△HCD的中位线MN.
∵CD=12-2-2=8,
∴MN=4,即G的移动路径长为4.
故③EF的中点G移动的路径长为4,正确;
∵G为EF的中点,∠EPF=90°,
∴①△EFP的外接圆的圆心为点G,正确.
∴①③正确.
∵点P从点C沿线段CD向点D运动(运动到点D停止),易证∠EPF=90°,所以四边形面积便是三个直角三角形的面积和,设cp=x,则四边形面积S=$\frac{{x}^{2}-8x+124}{4}$
∴AP不断增大,
∴四边形的面积S也会随之变化,故②错误.
④等腰Rt△APE和等腰Rt△PBF,
∠EPF=90°,
AP=$\sqrt{2}$PE,BP=$\sqrt{2}$PF,
当AP=AC=2时,即PE=$\sqrt{2}$,PF=5$\sqrt{2}$,
S△PEF最小=$\frac{1}{2}$PE•PF=5,故④错误;
故选:B.
点评 本题考查了等腰直角三角形的性质,平行四边形的判定与性质,三角形外接圆的知识以及三角形中位线的性质等知识.此题综合性很强,图形也很复杂,解题时要注意数形结合思想的应用.此题属于动点问题,是中考的热点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
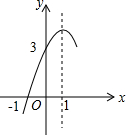 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
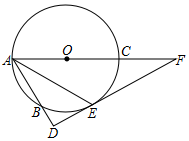 如图,AC为⊙O的直径,DAB为⊙O的割线,E为⊙O上一点,弧BE=弧CE,DE⊥AB于D,交AO的延长线于F
如图,AC为⊙O的直径,DAB为⊙O的割线,E为⊙O上一点,弧BE=弧CE,DE⊥AB于D,交AO的延长线于F查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×107 | B. | 30×106 | C. | 0.3×108 | D. | 3×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
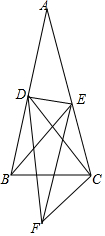 在△ABC中,AB=AC,∠A=20°,D、E分别为AB、AC上一点,AD=CD,∠ABE=30°.将CE绕点C逆时针旋转一定角度到F点,使得∠BED=2∠BCF,链接EF和DF,求DE、DF、CD三者的数量关系.
在△ABC中,AB=AC,∠A=20°,D、E分别为AB、AC上一点,AD=CD,∠ABE=30°.将CE绕点C逆时针旋转一定角度到F点,使得∠BED=2∠BCF,链接EF和DF,求DE、DF、CD三者的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
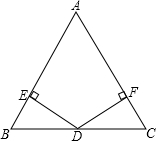 【原题再现】课本第81页课内练习第1题:如图,在△ABC中,D为BC边上一点,DB=DC,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:AB=AC.
【原题再现】课本第81页课内练习第1题:如图,在△ABC中,D为BC边上一点,DB=DC,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com