
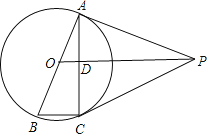
【题目】如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
【1】猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
【2】求证:PC是⊙O的切线
【答案】
【1】见解析
【2】见解析
【解析】(1)由已知得出OD是△ABC的中位线,从而得出结论
(2) 连接OC,证得△OAP≌△OCP,得出∠OCP=∠OAP,从而得出结论
(1)猜想:OD∥BC,CD=![]() BC.
BC.
证明:∵OD⊥AC,
∴AD=DC
∵AB是⊙O的直径,
∴OA=OB
∴OD是△ABC的中位线,
∴OD∥BC,OD=![]() BC
BC
(2)证明:连接OC,设OP与⊙O交于点E.
∵OD⊥AC,OD经过圆心O,
∴![]() ,即∠AOE=∠COE
,即∠AOE=∠COE
在△OAP和△OCP中,
∵OA=OC,OP=OP,
∴△OAP≌△OCP,
∴∠OCP=∠OAP
∵PA是⊙O的切线,
∴∠OAP=90°.
∴∠OCP=90°,即OC⊥PC
∴PC是⊙O的切线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
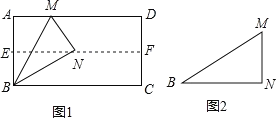
【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技实践社团制作实践设备,小明的操作过程如下:
①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;
②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);
③用一细橡胶棒连接C、D两点(如图3);
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为( )

A. 2![]() 分米 B. 2
分米 B. 2![]() 分米 C. 3
分米 C. 3![]() 分米 D. 3
分米 D. 3![]() 分米
分米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件![]() 为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
![]() 求出月销售量
求出月销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出月销售利润
求出月销售利润![]() 万元
万元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若该月销售利润为480万元,求此时的月销售量和销售单价各是多少元?
若该月销售利润为480万元,求此时的月销售量和销售单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
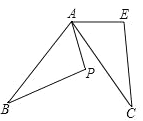
【题目】(1)解方程x2﹣4x=12;
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,
的中点,![]() 是直角三角形,
是直角三角形,![]() .
.![]() 保持不动,将
保持不动,将![]() 沿射线
沿射线![]() 向左平移,平移过程中点
向左平移,平移过程中点![]() 始终在射线
始终在射线![]() 上,且保持
上,且保持![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() .
.
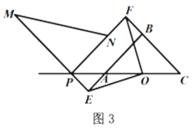
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
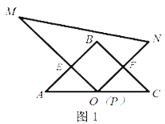
(2)如图2,当点![]() 在线段
在线段![]() 上时,猜想
上时,猜想![]() 与
与![]() 有怎样的数量关系与位置关系,并对你的猜想结果给予证明;
有怎样的数量关系与位置关系,并对你的猜想结果给予证明;
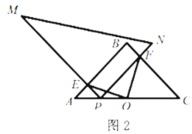
(3)如图3,当点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,则
,则![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
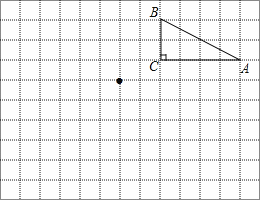
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;
(3)作出△ABC关于直线l对称的△A3B3C3,使A,B,C的对称点分别是A3,B3,C3;
(4)△A2B2C2与△A3B3C3成_____________,△A1B1C1与△A2B2C2成_____________(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点P的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
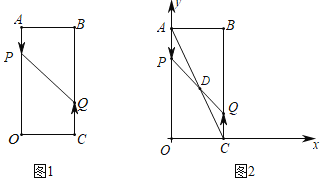
(1)当出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P、Q两点的距离为 cm;当运动时间为4s时,P、Q两点的距离为 cm;
(3)探索发现:如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连接AC,与PQ相交于点D,若双曲线y=![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com