
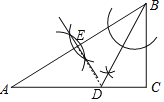
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹)
(2)连接DE,求证:△ADE≌△BDE。

【答案】(1)作图见解析;(2)证明见解析.
【解析】(1)①以B为圆心,任意长为半径画弧,交AB、BC于F、N,再以F、N为圆心,大于![]() FN长为半径画弧,两弧交于点M,过B、M作射线,交AC于D,线段BD就是∠B的平分线。
FN长为半径画弧,两弧交于点M,过B、M作射线,交AC于D,线段BD就是∠B的平分线。
②分别以A、B为圆心,大于![]() AB长为半径画弧,两弧交于X、Y,过X、Y作直线与AB
AB长为半径画弧,两弧交于X、Y,过X、Y作直线与AB
交于点E,点E就是AB的中点.
(2)首先根据角平分线的性质可得∠ABD的度数,从而得到∠ABD=∠A,根据等角对等边可得AD=BD,再加上条件AE=BE,即可利用SAS证明△ADE≌△BDE.
解:(1)作图如下:
(2)证明:∵∠ABD=![]() ×60°=30°,∠A=30°,
×60°=30°,∠A=30°,
∴∠ABD=∠A。∴AD=BD.
又∵AE=BE,
∴△ADE≌△BDE(SAS).


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
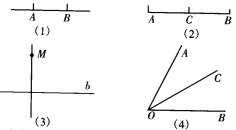
【题目】看图填空:
(1)过点________和点_______作直线;
(2)延长线段________到_________,且使________=_________.
(3)过点_________作直线_______的垂线;
(4)作射线_______,使_____平分∠________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( ) 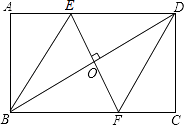
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一节”期间,小明一家自驾游去了离家240千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. 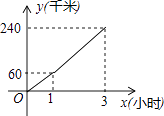
(1)求出y(千米)与x(小时)之间的函数表达式;
(2)他们出发2小时时,离目的地还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1 , 连接AC1 , 以AC1为边作第二个正方形AC1C2D2 , 则第10个正方形边长为( ) 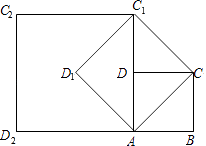
A.8
B.16
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去新华书店,如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图象 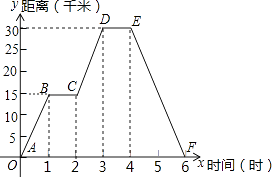
(1)根据图象回答:小明家离新华书店千米,小明用了小时到达新华书店;
(2)小明从家出发两个半小时走了千米;
(3)直线CD的函数解析式为;
(4)小明出发小时,离家12千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是5的相反数,c=|2|,且a、b、c分别是点A. B.C在数轴上对应的数.
(1)求a、b、c的值,并在数轴上标出点A. B. C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A. B.C三点的距离之和等于12,请直接写出所有点M对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=15,则S2的值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com