
 如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.
如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$. 分析 先连接CF,根据直线MN垂直平分CF,得到∠NCF=∠NFC,再根据BC∥AD,即可得到∠CBF=∠A=45°=∠EFN,判定△BNF是等腰直角三角形,根据Rt△BNF中,BF=$\sqrt{2}$BN=2$\sqrt{2}$,即可得出AF=AB+BF=2+2$\sqrt{2}$.
解答 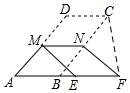 解:如图,连接CF,则直线MN垂直平分CF,
解:如图,连接CF,则直线MN垂直平分CF,
∴NC=NF,
∴∠NCF=∠NFC,
又∵BC∥AD,
∴∠CBF=∠A=45°=∠EFN,
∴△BNF是等腰直角三角形,
∴BN=NF=CN,
∴BN=CN=$\frac{1}{2}$BC=2,
∴Rt△BNF中,BF=$\sqrt{2}$BN=2$\sqrt{2}$,
∴AF=AB+BF=2+2$\sqrt{2}$.
故答案为:2+2$\sqrt{2}$.
点评 本题主要考查了折叠问题,等腰直角三角形以及平行四边形的性质的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
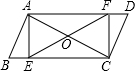 如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车次 | 出发站 | 到达站 | 出发时间 | 到达时间 |
| D5508 | 泰州 | 南京 | 08:53 | |
| K722 | 泰州 | 南京 | 20:04 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某课外学习小组为了了解本市城区某路段的汽车超速情况,他们在一段时间内随机测量了途径该路段汽车行驶的速度,整理并绘制出以下不完整的统计图表.
某课外学习小组为了了解本市城区某路段的汽车超速情况,他们在一段时间内随机测量了途径该路段汽车行驶的速度,整理并绘制出以下不完整的统计图表.| 数据段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | 0.18 |
| 50~60 | 78 | 0.39 |
| 60~70 | 56 | 0.28 |
| 70~80 | 20 | 0.10 |
| 总计 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com