
【题目】已知,∠ABC=48°,P是∠ABC内一定点,D、E分别是射线BA、BC上的点,当△PDE的周长最小时,∠DPE的度数是__________.
【答案】84°
【解析】试题解析:如图作点P关于直线AB的对称点F,作点P关于直线BC的对称点G,连接FG交AB于D,交BC于E,则△PDE的周长最小.

设∠ABP=∠ABF=x,∠CBP=∠CBG=y,则x+y=48°,
∵BP=BF,
∴∠BPF=∠BFP=![]() (180°-2x)=90°-x.同法可得∠BPG=90°-y,
(180°-2x)=90°-x.同法可得∠BPG=90°-y,
∴∠FPG=180°-x-y=132°,
∴∠BFP+∠BGP=132°,
∵∠BFG+∠BGF=180°-96°=84°,
∴∠PFG+∠PGF=132°-84°=48°,
∵DF=DP,EP=EG,
∴∠DFP=∠DPF,∠EGP=∠EPG,
∴∠EDP=2∠DFP,∠DEP=2∠EGP,
∴∠PDE+∠PED=96°,
∴∠DPE=180°-96°=84°,
故答案为:84°.


科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知31=3,32=9,33=27,34=81,35=243,36=729,37=2187…….则3+32+33+34+…+32019的末位数字是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
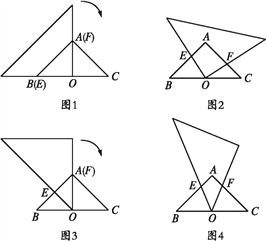
【题目】如图所示,在△ABC中,AB=AC=2,BC=2![]() ,∠A=90°.取一块含45°角的直角三角尺,将直角顶点放在斜边BC的中点O处,一条直角边过点A(如图1).三角尺绕点O顺时针方向旋转,使90°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图2).设BE=x,CF=y.
,∠A=90°.取一块含45°角的直角三角尺,将直角顶点放在斜边BC的中点O处,一条直角边过点A(如图1).三角尺绕点O顺时针方向旋转,使90°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图2).设BE=x,CF=y.
(1)探究:在图2中,线段AE与CF有怎样的大小关系?证明你的结论.
(2)求在上述旋转过程中y与x的函数表达式,并写出x的取值范围.
(3)若将直角三角尺45°角的顶点放在斜边BC边的中点O处,一条直角边过点A(如图3).三角尺绕O点顺时针方向旋转,使45°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图4).在三角尺绕点O旋转的过程中,△OEF是否能成为等腰三角形?若能,直接写出△OEF为等腰三角形时x的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )

A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面我们做一次折叠活动:

第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com