
抛物线
 过点
过点 ,顶点为M点.
,顶点为M点.

(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90˚.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90˚,说明理由.
(1)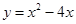 ;(2)
;(2)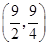 ;(3)存在.
;(3)存在.
【解析】
试题分析:(1)将A(1,-3),B(3,-3),C(-1,5)三点坐标代入y=ax2+bx+c中,列方程组求a、b、c的值,得出抛物线解析式;
(2)抛物线上存在一点P,使∠POM=90˚.设(a,a2-4a),过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F,利用互余关系证明Rt△OEP∽Rt△MFO,利用相似比求a即可;
(3)抛物线上必存在一点K,使∠OMK=90˚.过顶点M作MN⊥OM,交y轴于点N,在Rt△OMN中,利用互余关系证明△OFM∽△MFN,利用相似比求N点坐标,再求直线MN解析式,将直线MN解析式与抛物线解析式联立,可求K点坐标.
(1)根据题意,得
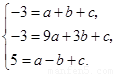
解得 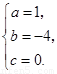
∴ 抛物线的解析式为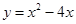 .
.
(2)抛物线上存在一点P,使∠POM=90˚.
x=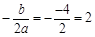 ,
,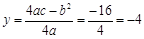 .
.
∴ 顶点M的坐标为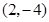 .
.
设抛物线上存在一点P,满足OP⊥OM,其坐标为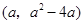 .
.
过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F.
则 ∠POE+∠MOF=90˚,∠POE+∠EPO=90˚.
∴ ∠EPO=∠FOM.
∵ ∠OEP=∠MFO=90˚,
∴ Rt△OEP∽Rt△MFO.
∴ OE∶MF=EP∶OF.
即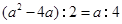 .
.
解,得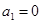 (舍去),
(舍去),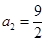 .
.
∴ P点的坐标为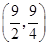 .
.
(3)

过顶点M作MN⊥OM,交y轴于点N.则 ∠FMN+∠OMF=90˚.
∵ ∠MOF+∠OMF=90˚,
∴ ∠MOF=∠FMN.
又∵ ∠OFM=∠MFN=90˚,
∴ △OFM∽△MFN.
∴ OF∶MF=MF∶FN. 即 4∶2=2∶FN.∴ FN=1.
∴ 点N的坐标为(0,-5).
设过点M,N的直线的解析式为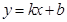 .
.
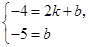 解,得
解,得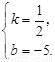 直线的解析式为
直线的解析式为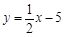 .
.
∴ 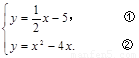 把①代入②,得
把①代入②,得 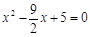 .
.
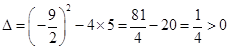 .
.
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点K,使∠OMK=90˚.
考点:本题考查了二次函数的综合运用
点评:解答本题的关键关键是通过已知三点求抛物线解析式,根据垂直关系证明三角形相似,得出线段长及点的坐标,利用直线解析式及抛物线解析式求满足条件的点的坐标.


科目:初中数学 来源: 题型:
 已知一抛物线过点O(0,0),A(6,0),B(4,3),
已知一抛物线过点O(0,0),A(6,0),B(4,3),查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013届四川省成都铁中九年级一诊模拟考试数学试卷(带解析) 题型:解答题
已知,如图1,抛物线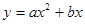 过点
过点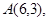 且对称轴为直线
且对称轴为直线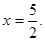 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.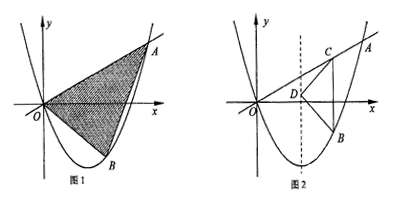
(1)求该抛物线的解析式:
(2)若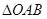 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)如图2,过点B作直线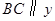 轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使
轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使 是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年四川省九年级一诊模拟考试数学试卷(解析版) 题型:解答题
已知,如图1,抛物线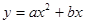 过点
过点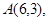 且对称轴为直线
且对称轴为直线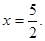 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.

(1)求该抛物线的解析式:
(2)若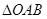 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)如图2,过点B作直线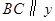 轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使
轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使 是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com