
科目:初中数学 来源: 题型:
一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
A.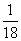 B.
B.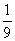 C.
C.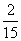 D.
D. 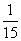
查看答案和解析>>
科目:初中数学 来源: 题型:
【问题】如图1、2是底面为1cm,母线长为2cm的圆柱体和圆锥体模型.现要用长为2πcm,宽为4cm的长方形彩纸(如图3)装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套,长方形彩纸共有122张,用这些纸最多能装饰多少套模型呢?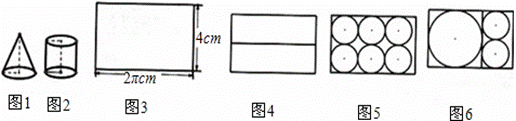
【对话】老师:“长方形纸可以怎么裁剪呢?”
学生甲:“可按图4方式裁剪出2张长方形.”
学生乙:“可按图5方式裁剪出6个小圆.”
学生丙:“可按图6方式裁剪出1个大圆和2个小圆.”
老师:尽管还有其他裁剪方法,但为裁剪方便,我们就仅用这三位同学的裁剪方法!
【解决】(1)计算:圆柱的侧面积是 4πcm2,圆锥的侧面积是 2cm2.
(2)1张长方形彩纸剪拼后最多能装饰 2个圆锥模型;5张长方形彩纸剪拼后最多能装饰 6个圆柱体模型.
(3)求用122张彩纸对多能装饰的圆锥、圆柱模型套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
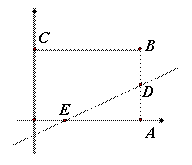
如图,矩形OABC顶点A(6,0)、C(0,4),直线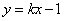 分别交BA、OA于点D、E,且D为BA中点。
分别交BA、OA于点D、E,且D为BA中点。
(1)求k的值及此时△EAD的面积;
(2)现向矩形内随机投飞镖,求飞镖落在△EAD内的概率。(若投在边框上则重投)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,O是坐标原点,直线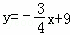 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线 经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
(1)求抛物线的解析式及点A的坐标;
(2)以OC为直径的⊙O′与BC交于点M,当t为何值时,PM与⊙O′相切?请说明理由.
(3)在点P从点A出发的同时,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒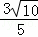 个单位长度的速度向点A运动,运动时间和点P相同.
个单位长度的速度向点A运动,运动时间和点P相同.
①记△BPQ的面积为S,当t为何值时,S最大,最大值是多少?
②是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.
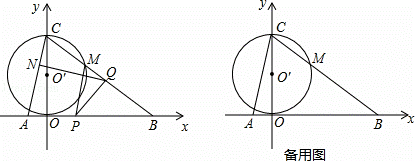
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com