
分析 (1)运用二次根式有意义的条件,即$\sqrt{1-4x}$,$\sqrt{4x-1}$必须同时根号下部分大于等于0,即1-4x≥0,且4x-1≥0,得出x的值,再代入y=$\sqrt{1-4x}$+$\sqrt{4x-1}$+$\frac{1}{2}$,求出y的值,从而得出代数式的值;
(2)把分子、分母分解因式,把除法化成乘法,约分化简即可.
解答 解:(1)∵y=$\sqrt{1-4x}$+$\sqrt{4x-1}$+$\frac{1}{2}$,
∴1-4x≥0,且4x-1≥0,
∴x=$\frac{1}{4}$,
∴y=$\frac{1}{2}$,
∴$\sqrt{\frac{x}{y}+2+\frac{y}{x}}$-$\sqrt{\frac{x}{y}-2+\frac{y}{x}}$=$\sqrt{\frac{1}{2}+2+2}$-$\sqrt{\frac{1}{2}-2+2}$=$\frac{3\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=$\sqrt{2}$;
(2)$\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}$+$\frac{\sqrt{a}}{a-b}$•$\frac{a+2\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}$÷($\sqrt{a}$+$\sqrt{b}$)=$\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}$+$\frac{\sqrt{a}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$•$\frac{(\sqrt{a}+\sqrt{b})^{2}}{\sqrt{a}+\sqrt{b}}$•$\frac{1}{\sqrt{a}+\sqrt{b}}$=$\frac{\sqrt{b}(\sqrt{a}+\sqrt{b})+\sqrt{a}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$=$\frac{\sqrt{ab}+b+\sqrt{a}}{a-b}$.
点评 此题主要考查了二次根式的化简求值,二次根式有意义的条件,以及二次根式的混合运算,解决问题的关键是根据$\sqrt{1-4x}$,$\sqrt{4x-1}$同时有意义,即1-4x≥0,且4x-1≥0,从而得出x的值.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
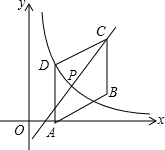 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
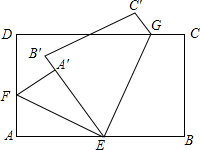 如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.
如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com