
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度![]() ,那么这个月应缴纳电费多少元?(用含a的代数式表示)
,那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果这个月缴纳电费为147.8元,那么小张家这个月用电多少度?
【答案】解:(1) ![]() ----------2分
----------2分
答: 这个月应缴纳电费64元. ----------3分
(2)![]() ----------6分
----------6分
![]()
![]() ----------8分
----------8分
答:如果小张家一个月用电a度![]() ,那么这个月应缴纳电费
,那么这个月应缴纳电费![]() 元. ----------9分
元. ----------9分
(3) ![]() ----------11分
----------11分
解得 ![]() ----------13分
----------13分
答:如果这个月缴纳电费为147.8元,那么小张家这个月用电241度. ----------14分
【解析】(1)如果小张家一个月用电128度.128<150,所以只有一种情况,每度电0.5元,可求解.
(2)a>150,两种情况都有,先算出128度电用的钱,再算出剩下的(a-128)度的电用的钱,加起来就为所求.
(3)147.8>128×0.5,所以所用的电超过了128度电,和2中的情况类似,设此时用电a度,可列方程求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度得到点A′,则点A′的坐标是( )
A. (3,3) B. (-1,3) C. (-1,-1) D. (3,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
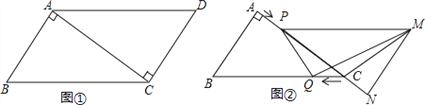
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() ,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
(1)求点B的坐标.
(2)若t=1时,连接BQ,求△ABQ的面积.
(3)如图2,以PQ为直径作⊙I,记⊙I与射线AC的另一个交点为E.
① 若![]() ,求此时t的值.
,求此时t的值.
② 若圆心I在△ABC内部(不包含边上),则此时t的取值范围为 .(直接写出答案)
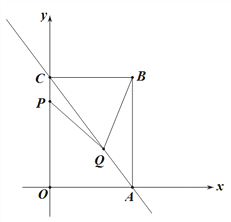
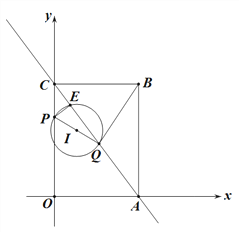
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com