
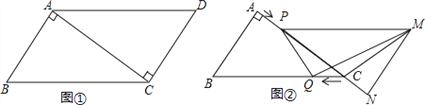
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
【答案】t=![]() ;y=-
;y=-![]() ;1:4;t=
;1:4;t=![]()
【解析】试题分析: ![]() 当PQ∥MN时,可得:
当PQ∥MN时,可得: ![]() ,从而得到:
,从而得到: ![]() ,解方程求出
,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,则可以得到
,则可以得到![]() ,根据相似三角形的性质可以求出
,根据相似三角形的性质可以求出![]() ,
, ![]() ,利用三角形的面积公式求出
,利用三角形的面积公式求出![]() 与
与![]() 的关系式;
的关系式;
![]() 根据S△QMC:
根据S△QMC: ![]() 可以得到关于
可以得到关于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,则△CPD∽△CBA,利用相似三角形的性质可以得到:
,则△CPD∽△CBA,利用相似三角形的性质可以得到: ![]() ,解方程求出
,解方程求出![]() 的值.
的值.
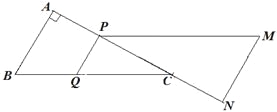
试题解析:(1)如图所示,
若PQ∥MN,则有![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() .
.
(2)如图所示,
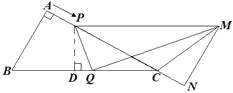
作![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴△QMC的面积为: ![]()
(3)存在![]() 时,使得S△QMC:
时,使得S△QMC: ![]() .
.
理由如下:
∵PM∥BC
∴![]()
∵S△QMC: ![]() ,
,
∴S△PQC: S△ABC=1:5,
∵![]()
.∴![]()
∴![]()
∴![]()
∴存在当![]() 时,S△QMC:
时,S△QMC: ![]() ;
;
(4)存在某一时刻![]() ,使
,使![]() .
.
理由如下:
如图所示,
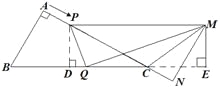
作![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() .
.
∵PQ⊥MQ,
∴△PDQ∽△QEM,
∴![]() ,
,
即![]()
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
, ![]() (舍去)
(舍去)
∴当![]() 时,使PQ⊥MQ.
时,使PQ⊥MQ.


科目:初中数学 来源: 题型:
【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度![]() ,那么这个月应缴纳电费多少元?(用含a的代数式表示)
,那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果这个月缴纳电费为147.8元,那么小张家这个月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市展览馆某天四个时间段进出馆人数统计如下表,则馆内人数变化最大的时间段为_______________.
9:00-10:00 | 10:00-11:00 | 14:00-15:00 | 15:00-16:00 | |
进馆人数 | 50 | 24 | 55 | 32 |
出馆人数 | 30 | 65 | 28 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com