
����Ŀ����ͼ���ڵ�1����ABA1������B=40������BAA1=��BA1A����A1B��ȡһ��C���ӳ�AA1��A2��ʹ���ڵ�2����A1CA2������A1CA2=��A1 A2C����A2C��ȡһ��D���ӳ�A1A2��A3��ʹ���ڵ�3����A2DA3������A2DA3=��A2 A3D��������������������ȥ����3������������A3Ϊ������ڽǵĶ���Ϊ ����n������������AnΪ������ڽǵĶ���Ϊ ��

���𰸡�17.5��@![]() ��
��
������������������ȸ��ݵ��������ε����������BA1A�Ķ������ٸ�����������ǵ����ʼ����������ε����ʷֱ������CA2A1����DA3A2����EA4A3�Ķ������ҳ����ɼ��ɵó���n�������ε���AnΪ����ĵǵĶ�����
�⣺���ڡ�ABA1�У���B=40�㣬AB=A1B��
���BA1A=![]() (180��-40��)=70�㣬
(180��-40��)=70�㣬
��A1A2=A1C����BA1A�ǡ�A1A2C����ǣ�
���CA2A1=����BA1A=����70��=35�㣻
ͬ���ɵã���DA3A2=![]() ��70��=17.5�㣬��EA4A3=
��70��=17.5�㣬��EA4A3=![]() ��70�㣬
��70�㣬
�Դ����ƣ���n�������ε���AnΪ����ĵǵĶ���=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
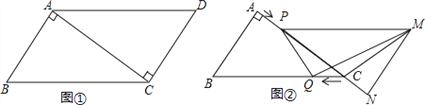
����Ŀ����֪����ͼ�٣���ABCD�У�AB=3cm��BC=5cm��AC��AB����ACD��AC�ķ�������ƽ�Ƶõ���PNM���ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�C��������CB���������ƶ����ٶ�Ϊ1cm/s������PNMֹͣƽ��ʱ����QҲֹͣ�ƶ�����ͼ�ڣ����ƶ�ʱ��Ϊt��s����0��t��4��������PQ��MQ��MC������������⣺
��1����tΪ��ֵʱ��PQ��MN��
��2�����QMC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS��QMC��S�ı���ABQP=1��4�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4���Ƿ����ijһʱ��t��ʹPQ��MQ�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=kx��ͼ����A����1��2�����������������Ľ���ʽΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
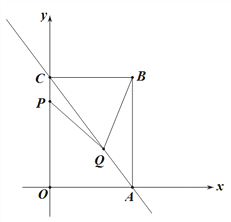
����Ŀ����ͼ1��ֱ��![]() ����x�ᡢy��ֱ��ڵ�A��C����ACΪ�Խ���������OABC����P��Q�ֱ�Ϊ����OC������AC�ϵĶ��㣬����AQ=2CP, ����PQ�����P������ΪP��0��t��.
����x�ᡢy��ֱ��ڵ�A��C����ACΪ�Խ���������OABC����P��Q�ֱ�Ϊ����OC������AC�ϵĶ��㣬����AQ=2CP, ����PQ�����P������ΪP��0��t��.
��1�����B������.
��2����t=1ʱ������BQ�����ABQ�����.
��3����ͼ2����PQΪֱ������I���ǡ�I������AC����һ������ΪE.
�� ��![]() �����ʱt��ֵ.
�����ʱt��ֵ.
�� ��Բ��I�ڡ�ABC�ڲ������������ϣ������ʱt��ȡֵ��ΧΪ .��ֱ��д���𰸣�
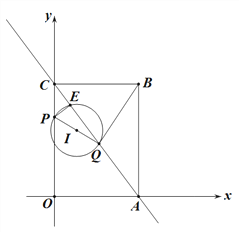
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������ӵ�ֱ���� 1 ���ף�1 ����= 0.000 000 001�ף�������������ӵ�ֱ�� 1 �����ÿ�ѧ�������ɱ�ʾΪ( )
A. 0.110-8�� B. 1109�� C. 10 10-10�� D. 110-9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
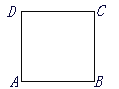
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3���Զ���AΪԭ�㣬����һ���ڱ����������غϣ����������ABCD�������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x����1�ǹ���x�ķ���2x+a��1�Ľ⣬��a��ֵΪ( )
A. ��1B. 3C. 1D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������� y 3x ������˵����ȷ����( )
A. y �� x ���������С B. y �� x �����������
C. y �� x �ļ�С������ D. y ����Сֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com