
【题目】在等边![]() 中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
(1)如图1,若![]() ,求线段AD的长;
,求线段AD的长;
(2)如图2,若F是线段BD的中点,连接AF,若![]() ,求证:
,求证:![]() .
.
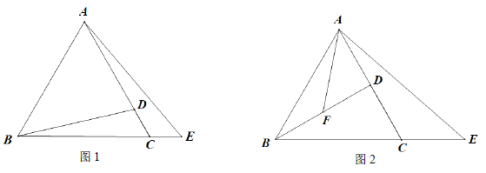
【答案】(1) ![]() ;(2)见解析
;(2)见解析
【解析】
(1)过点B作BM⊥AD于点G,根据等边三角形的性质,求出AM=3,BM=![]() 在Rt△AMB中,根据
在Rt△AMB中,根据![]() ,求出MD的长度,即可求出线段AD的长;
,求出MD的长度,即可求出线段AD的长;
(2)延长AF至点N使得FN=AF,连接BN,先证明出△ADF≌△NBF,得出DA=BN,∠DAF=∠N,进而得出∠N=∠E,再用AAS判断出△ABN≌△ACE即可得出结论;
(1) 过点B作BM⊥AD于点G
∵△ABC是等边三角形,
∴AM=3,BM=![]()
在Rt△AMB中,![]()
∴MD=![]()
∴AD=AM+MD=![]()
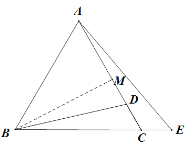
(2) 延长AF至点N使得FN=AF,连接BN
∵ F是BD的中点
∴BF=DF
在△ADF和△NBF中:
 ,
,
∴△ADF≌△NBF(SAS),
∴DA=BN,∠DAF=∠N
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°
∵∠EAF=60°,
∴∠BAF=∠DAE
∵∠EAF=∠EAC+∠DAF=60°,∠ACD=∠EAC+∠E=60°,
∴∠DAF=∠E,
∴∠N=∠E
在△ABN和△ACE中:
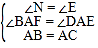 ,
,
∴△ABN≌△ACE(AAS),∴BN=CE,∴AD=DC,∴BD⊥AC,∴BD=![]()


科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
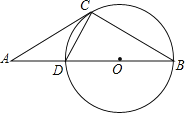
【题目】如图,已知直线AC与⊙O相交于点C,直线AO与⊙O相交于D,B两点.已知∠ACD=∠B.
(1)求证:AC是⊙O的切线;
(2)若AC=6,AD=4,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的高,且
的高,且![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点E在AD上,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若BE=BC,求
,若BE=BC,求![]() 的大小;
的大小;
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
图1.  图2.
图2.  图3.
图3. 
查看答案和解析>>
科目:初中数学 来源: 题型:
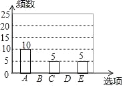
【题目】随着移动终端设备的升级换代,手机己经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天:B.学习:C.购物:D.游戏:E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 20% |
C | 5 | 10% |
D | p | 40% |
E | 5 | 10% |
合计 | 100% |
根据以上信息解答下列问题:
(1)m= ,n= ,p= ;
(2)补全条形统计图;
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
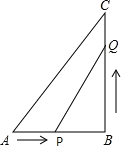
【题目】已知:如图所示.在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.

A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com