
【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在一次函数关系.从温度计的刻度上可以看出,摄氏温度x(℃)与华氏温度y(℉)有如下的对应关系:
x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
(1)试确定y与x之间的函数关系。
(2)某天,滨海的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
【答案】(1)y=1.8x+32.(2)这一天澳大利亚悉尼的最高气温较高.
【解析】
试题分析:(1)根据题意可知摄氏温度与华氏温度之间存在一次函数关系,从而可以设出一次函数的解析式,根据表格中的数据可以求出一次函数的解析式;
(2)将x=25代入第一问中求得的函数解析式,可以将滨海的温度转化为华氏温度,从而可以和悉尼的最高气温进行比较,进而得到本题的答案.
试题解析:(1)设摄氏温度与华氏温度之间的一次函数关系是y=kx+b,
∵由表格可得,x=0时,y=32;x=10时,y=50.
∴![]() .
.
解得,k=1.8,b=32.
∴y与x之间的函数关系式是:y=1.8x+32.
(2)将x=25代入y=1.8x+32得,y=1.8×25+32=45+32=77.
∵77<80,
∴悉尼的最高气温较高.
答:这一天澳大利亚悉尼的最高气温较高.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有两个角为直角的四边形是矩形
B.矩形的对角线互相垂直
C.平行四边形的对角线互相平分
D.对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】起重机将质量为6.5t的货物沿竖直方向提升了2m,则起重机提升货物所做的功用科学记数法表示为(g=10N/kg)
A.1.3×106J B.13×105JC.13×104J D.1.3×105J
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区今年共有1.4万名七年级学生参加期末考试,为了了解这1.4万名学生的数学成绩,从中抽取了1000名学生的数学成绩进行统计分析,以下说法正确的有( )个
①这种抽查采用了抽样调查的方式
②1.4万名学生的数学成绩是总体
③1000名学生是总体的一个样本
④每名学生的数学成绩是总体的一个样本.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=![]() ,则
,则![]() = ;
= ;
(2)若y2=![]() ,则
,则![]() = ;
= ;
(3)若y3=![]() ,则
,则![]() = ;
= ;
(4)由以上探究可知,y2012=![]() ,
,![]() 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
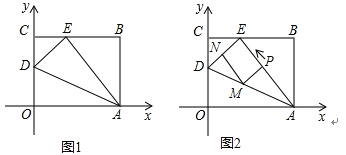
(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果品批发公司以16元/千克购进一批樱桃.由往年市场销售情况的统计分析可知:当销售价定为25 元/千克时,每天可售出1 000 千克;若销售价定为20元/千克时,每天可售出2000千克.假设每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品无积压且不考虑其他因素的条件下,销售价格定为多少时,才能使每天的销售毛利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
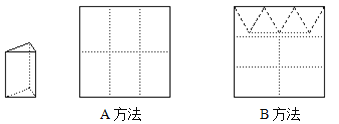
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com