

分析 (1)用k表示点B坐标得到(2k,2k),代入抛物线解析式求出k即可.
(2)设点E坐标为(m,$\frac{1}{4}$m2+1),求出EF、DE(用k表示),即可解决问题.
解答 解:(1)由题意点C坐标(0,k),
∵OC=CD,
∴点D坐标为(0,2k),
∵AB=20D,A、B关于y轴对称,
∴点B坐标为(2k,2k),
∴2k=$\frac{1}{4}$•(2k)2+k,
∴k=1或0(舍弃),
∴抛物线解析式为y=$\frac{1}{4}$x2+1.
(2)设点E坐标为(m,$\frac{1}{4}$m2+1),
∵EF⊥x轴,D(0,2)
∴EF=$\frac{1}{4}$m2+1,
DE=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\sqrt{(\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}$m2+1,
∴DE=EF,
∴$\frac{EF}{DE}$=1.
点评 本题考查待定系数法求二次函数解析式、勾股定理、两点之间的距离公式等知识,解题的关键是学会用参数表示相应点的坐标,把问题转化为方程解决,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,给出如下定义:形如y=(x-m)(x-m+1)与y=(x-m)(x-m-1)的两个二次函数的图象叫做兄弟抛物线.
在平面直角坐标系中,给出如下定义:形如y=(x-m)(x-m+1)与y=(x-m)(x-m-1)的两个二次函数的图象叫做兄弟抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
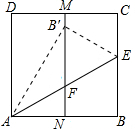 如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
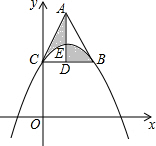 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com