
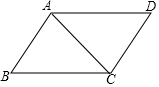
 如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
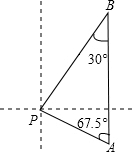 在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)
在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com