
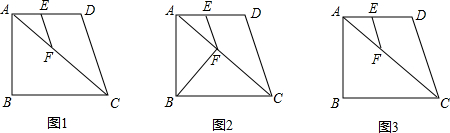
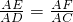 ,AE=t,CF=2t,
,AE=t,CF=2t,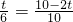 ,解得
,解得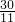
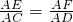
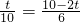 解得:
解得:

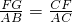 ,EG=AB=6
,EG=AB=6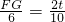 ,
,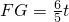
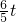 ,
, t)2=(10-2t)2,解得
t)2=(10-2t)2,解得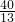 ,t2=
,t2= (不符合题意应舍去)
(不符合题意应舍去)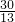 ,AE=
,AE=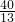
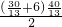
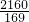 cm2
cm2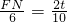
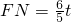 ,
,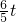 ,
,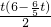
 (t-
(t- )2+
)2+ .
. 时,S△AFE最大,最大值是
时,S△AFE最大,最大值是 .
.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:初中数学 来源: 题型:
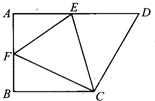 12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=
12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=查看答案和解析>>
科目:初中数学 来源: 题型:
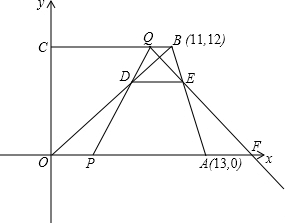 为t(单位:秒).
为t(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( )
(2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究:
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com