

分析 (1)①△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积实际是大扇形BAC与小扇形BPP′的面积差,且这两个扇形的圆心角同为90度;
②连接PP′,证△PBP′为等腰直角三角形,从而可在Rt△PP′C中,用勾股定理求得PC=6;
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股定理的逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.
解答 (1)解:①∵△PAB绕点B顺时针旋转90°到△P′CB,如图1所示:
∴S△ABP=S△BP′C ,
∴S阴影=S扇形ABC+S△BP′C-S扇形PBP′-S△ABP
=S扇形ABC-S扇形PBP′
=$\frac{90π({a}^{2}-{b}^{2})}{360}$
=$\frac{π}{4}$(a2-b2);
②连接PP′,
如图2所示: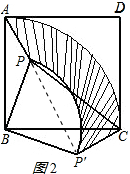
根据旋转的性质可知:
BP=BP′,∠PBP′=90°,
即:△PBP′为等腰直角三角形,
∴∠BPP′=45°,
∵∠BPA=∠BP′C=135°,∠BP′P=45°,
∴∠BPA+∠BPP′=180°,
即A、P、P′共线,
∴∠PP′C=135°-45°=90°;
在Rt△PP′C中,PP′=4$\sqrt{2}$,P′C=PA=2,
根据勾股定理可得PC=$\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6;
(2)证明:连接PP′,如图3所示: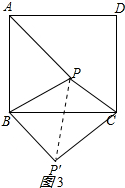
∵△PAB绕点B顺时针旋转90°到△P′CB,
∴PA=P′C,
由(1)①可知:△BPP′是等腰直角三角形,
即PP′2=2PB2,
∵PA2+PC2=2PB2=PP′2,
∴PC2+P′C2=PP′2,
∴∠P′CP=90°;
∵∠PBP′=∠PCP′=90°,
∴在四边形BPCP′中,∠BP′C+∠BPC=180°;
∵∠BPA=∠BP′C,
∴∠BPC+∠APB=180°,
即点P在对角线AC上.
点评 本题四边形综合题目,考查了正方形的性质、旋转的性质、勾股定理、勾股定理的逆定理、等腰直角三角形的判定与性质、扇形的面积公式等知识;本题综合性强,难度较大,熟练掌握旋转的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A、B、C三地依次为同一高速公路上的三个城市,某天,甲、乙两车分别从A地、C地同时出发,匀速前进,并相约同时到达B地,甲车匀速行驶一段时间后,中途因故停留一段时间后,再以另一速度匀速前进,结果甲乙两车仍恰好在相约时间到达B地,如图y1、y2分别是甲、乙两车行驶的路程y(km)与所用时间x(h)的函数图象.求A、B两地距离.
A、B、C三地依次为同一高速公路上的三个城市,某天,甲、乙两车分别从A地、C地同时出发,匀速前进,并相约同时到达B地,甲车匀速行驶一段时间后,中途因故停留一段时间后,再以另一速度匀速前进,结果甲乙两车仍恰好在相约时间到达B地,如图y1、y2分别是甲、乙两车行驶的路程y(km)与所用时间x(h)的函数图象.求A、B两地距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
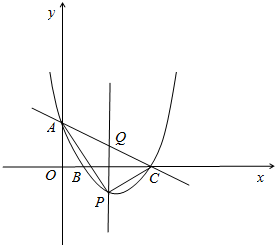 如图,在平面直角坐标系中,抛物线y=$\frac{4}{5}$x2-$\frac{24}{5}$x+4交y轴于点A,交x轴于B、C两点且B在C左边.设点P是直线AC下方抛物线上的点(不与A、C重合),过P作PQ∥y轴交线段AC于Q,若点P的横坐标为x,连接PA、PC.
如图,在平面直角坐标系中,抛物线y=$\frac{4}{5}$x2-$\frac{24}{5}$x+4交y轴于点A,交x轴于B、C两点且B在C左边.设点P是直线AC下方抛物线上的点(不与A、C重合),过P作PQ∥y轴交线段AC于Q,若点P的横坐标为x,连接PA、PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
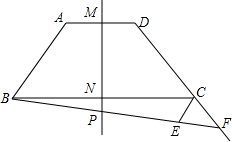 已知等腰梯形ABCD中,AD∥BC,AD=4,BC=10,AB=CD=5,直线MN是等腰梯形的对称轴,P是射线MN上一点,射线BP交射线DC于点F,过C点作CE∥AB,与射线BP交于点E.
已知等腰梯形ABCD中,AD∥BC,AD=4,BC=10,AB=CD=5,直线MN是等腰梯形的对称轴,P是射线MN上一点,射线BP交射线DC于点F,过C点作CE∥AB,与射线BP交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com