
分析 首先化简($\frac{{{x^2}-2x+1}}{{{x^2}-x}}$+$\frac{{{x^2}-4}}{{{x^2}+2x}}$)÷$\frac{1}{x}$,然后根据x为满足-3<x<2的整数,求出x的值,再根据x的取值范围,求出算式的值是多少即可.
解答 解:($\frac{{{x^2}-2x+1}}{{{x^2}-x}}$+$\frac{{{x^2}-4}}{{{x^2}+2x}}$)÷$\frac{1}{x}$
=[$\frac{{(x-1)}^{2}}{x(x-1)}$+$\frac{(x+2)(x-2)}{x(x+2)}$]×x
=($\frac{x-1}{x}$+$\frac{x-2}{x}$)×x
=2x-3
∵x为满足-3<x<2的整数,
∴x=-2,-1,0,1,
∵x要使原分式有意义,
∴x≠-2,0,1,
∴x=-1,
当x=-1时,
原式=2×(-1)-3=-5
点评 此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )| A. | △AEE′是等腰直角三角形 | B. | AF垂直平分EE' | ||
| C. | △E′EC∽△AFD | D. | △AE′F是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
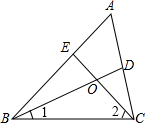 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
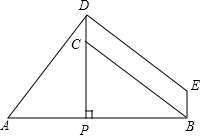 如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.
如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com