
分析 (1)(2)先去括号合并化简,再进一步代入数值求得答案即可;
(3)先去括号合并化简,利用含x的项为0,求得a、b,进一步化简代数式,代入数值求得答案即可.
解答 解:(1)原式=$\frac{3}{2}$m-$\frac{5}{2}$m+1+12-3m
=-4m+13
当m=-3时,
原式=25;
(2)原式=5a2b-[2a2b-2ab2+4a2b]-2ab2
=5a2b-6a2b+2ab2-2ab2
=-a2b
当a=-$\frac{1}{2}$,b=4时,
原式=-1;
(3)(2x2+ax-y+1)-(2bx2-3x+5y-4)
=2x2+ax-y+1-2bx2+3x-5y+4
=(2-2b)x2+(a+3)x-6y+5
∵代数式的值与字母x所取的值无关,
∴2-2b=0,a+3=0
∴a=-3 b=1;
则-$\frac{1}{3}{a^3}-2{b^2}-({\frac{1}{4}{a^3}-3{b^2}})$
=-$\frac{7}{12}$a3+b2
=$\frac{67}{4}$.
点评 此题考查整式的化简求值,掌握去括号的方法与合并同类项的方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
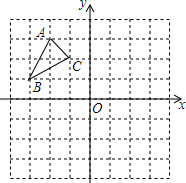 如图,△ABC中A(-2,3),B(-31),C(-1,2).
如图,△ABC中A(-2,3),B(-31),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com