
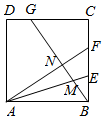
 如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=$\frac{4}{3}$NF;③$\frac{BM}{MG}$=$\frac{3}{8}$;④S四边形CGNF=$\frac{1}{2}$S四边形ANGD.其中正确的结论的序号是①③.
如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=$\frac{4}{3}$NF;③$\frac{BM}{MG}$=$\frac{3}{8}$;④S四边形CGNF=$\frac{1}{2}$S四边形ANGD.其中正确的结论的序号是①③. 分析 ①易证△ABF≌△BCG,即可解题;
②易证△BNF∽△BCG,即可求得$\frac{BN}{NF}$的值,即可解题;
③作EH⊥AF,令AB=3,即可求得MN,BM的值,即可解题;
④连接AG,FG,根据③中结论即可求得S四边形CGNF和S四边形ANGD,即可解题.
解答 解:①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠BCG=90°}\\{BF=CG}\end{array}\right.$,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,$\left\{\begin{array}{l}{∠CBG=∠NBF}\\{∠BCG=∠BNF=90°}\end{array}\right.$,
∴△BNF∽△BCG,∴$\frac{BN}{NF}$=$\frac{BC}{CG}$=$\frac{3}{2}$,
∴BN=$\frac{2}{3}$NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,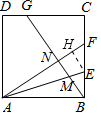
AF=$\sqrt{{AB}^{2}{+BF}^{2}}$=$\sqrt{13}$,
∵S△ABF=$\frac{1}{2}$AF•BN=$\frac{1}{2}$AB•BF,
∴BN=$\frac{6\sqrt{13}}{13}$,NF=$\frac{2}{3}$BN=$\frac{4\sqrt{13}}{13}$,
∴AN=AF-NF=$\frac{9\sqrt{13}}{13}$,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=$\frac{3\sqrt{13}}{13}$,NH=$\frac{2\sqrt{13}}{13}$,BN∥EH,
∴AH=$\frac{11\sqrt{13}}{13}$,$\frac{AN}{AH}$=$\frac{MN}{EH}$,解得:MN=$\frac{27\sqrt{13}}{143}$,
∴BM=BN-MN=$\frac{3\sqrt{13}}{11}$,MG=BG-BM=$\frac{8\sqrt{13}}{11}$,
∴$\frac{BM}{MG}$=$\frac{3}{8}$;③正确;
④连接AG,FG,根据③中结论,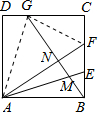
则NG=BG-BN=$\frac{7\sqrt{13}}{13}$,
∵S四边形CGNF=S△CFG+S△GNF=$\frac{1}{2}$CG•CF+$\frac{1}{2}$NF•NG=1+$\frac{14}{13}$=$\frac{27}{13}$,
S四边形ANGD=S△ANG+S△ADG=$\frac{1}{2}$AN•GN+$\frac{1}{2}$AD•DG=$\frac{63}{26}$+$\frac{3}{2}$=$\frac{51}{13}$,
∴S四边形CGNF≠$\frac{1}{2}$S四边形ANGD,④错误;
故答案为 ①③.
点评 本题考查了全等三角形的判定和性质,考查了相似三角形的判定和对应边比例相等的性质,本题中令AB=3求得AN,BN,NG,NF的值是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
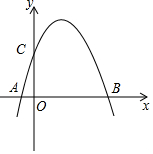 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 手机型号 | A型 | B型 |
| 进价(单位:元/部) | 900 | 1200 |
| 预售价(单位:元/部) | 1200 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
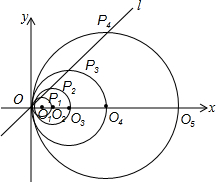 如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中$\widehat{{P}_{2017}{O}_{2018}}$的长为22015π..
如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中$\widehat{{P}_{2017}{O}_{2018}}$的长为22015π..查看答案和解析>>
科目:初中数学 来源: 题型:选择题
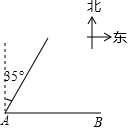 如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )| A. | 北偏东55° | B. | 北偏西55° | C. | 北偏东35° | D. | 北偏西35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a>-\frac{1}{8}$ | B. | $a≥-\frac{1}{8}$ | C. | $a>-\frac{1}{8}$且a≠1 | D. | $a≥-\frac{1}{8}$且a≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
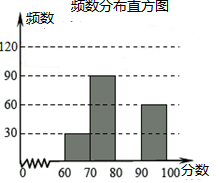 某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
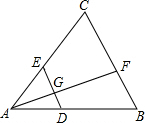 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{EC}$ | B. | $\frac{AG}{GF}$=$\frac{AE}{BD}$ | C. | $\frac{BD}{AD}$=$\frac{CE}{AE}$ | D. | $\frac{AG}{AF}$=$\frac{AC}{EC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com