
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,
那么x满足的方程是( )
A.100(1+x)2=81 B.100(1-x)2=81 C.100(1-x%)2=81 D.100x2=81
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣4,0),B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.
①如图(1),若四边形ODAE是以OA为对角线的平行四边形,当平行四边形ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
②如图(2),直线y=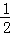 x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为
x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为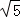 :2?若存在,请求出点D的坐标;若不存在,请说明理由.
:2?若存在,请求出点D的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
某同学报名参加运动会,有以下5个项目可供选择:
径赛项目:100m ,200m ,400m(分别用A1 、A2 、A3表示);
田赛项目:跳远 ,跳高(分别用B1 、B2表示).
⑴ 该同学从5个项目中任选一个,恰好是田赛项目的概率为 ;
⑵ 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.


查看答案和解析>>
科目:初中数学 来源: 题型:
已知:∥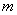 ∥
∥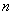 ∥,平行线与
∥,平行线与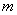 、
、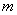 与
与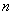 、
、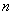 与之间的距离分别为
与之间的距离分别为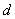 1、
1、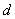 2、
2、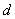 3,且
3,且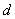 1 =
1 =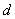 3 = 1,
3 = 1,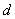 2 = 2 . 我们把四个顶点分别在、
2 = 2 . 我们把四个顶点分别在、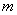 、
、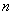 、这四条平行线上的四边形称为“格线四边形”.
、这四条平行线上的四边形称为“格线四边形”.
【探究1】 ⑴ 如图1,正方形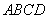 为“格线四边形”,
为“格线四边形”,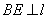 于点
于点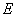 ,
,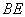 的反向延长线交直线于点
的反向延长线交直线于点 . 求正方形
. 求正方形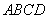 的边长.
的边长.
【探究2】 ⑵ 矩形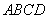 为“格线四边形”,其长 :宽 = 2 :1 ,则矩形
为“格线四边形”,其长 :宽 = 2 :1 ,则矩形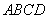 的宽为_____. (直接写出结果即可)
的宽为_____. (直接写出结果即可)
【探究3】 ⑶ 如图2,菱形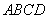 为“格线四边形”且∠
为“格线四边形”且∠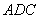 =60°,△
=60°,△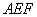 是等边三角形,
是等边三角形,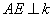 于点
于点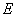 , ∠
, ∠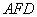 =90°,直线
=90°,直线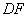 分别交直线、于点
分别交直线、于点 、
、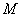 . 求证:
. 求证: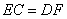 .
.
【拓 展】 ⑷ 如图3,∥,等边三角形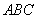 的顶点
的顶点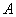 、
、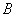 分别落在直线、上,
分别落在直线、上,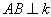 于点
于点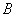 , 且
, 且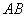 =4 ,∠
=4 ,∠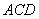 =90°,直线
=90°,直线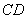 分别交直线、于点
分别交直线、于点 、
、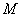 ,点
,点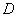 、
、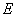 分别是线段
分别是线段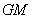 、
、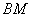 上的动点,且始终保持
上的动点,且始终保持 =
=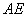 ,
,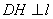 于点
于点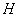 .
.
猜想: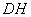 在什么范围内,
在什么范围内,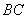 ∥
∥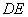 ?并说明此时
?并说明此时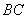 ∥
∥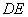 的理由.
的理由.
 |


查看答案和解析>>
科目:初中数学 来源: 题型:
驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|


查看答案和解析>>
科目:初中数学 来源: 题型:
如图2所示把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是 ( )

图2
(A)正三角形 (B)正方形 (C)正五边形 (D)正六边形


查看答案和解析>>
科目:初中数学 来源: 题型:
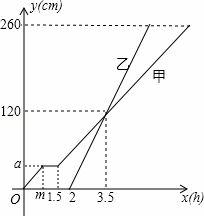
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com