

分析 (1)根据亮点(或暗点)的定义即可求得;
(2)根据亮点的定义列出方程,解方程即可.
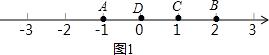
解答 解:(1)∵$\frac{2-(-2)}{4-2}$=2,$\frac{4-0}{0-(-2)}$=2,
∴【M,N】的亮点表示的数是2;【N,M】的亮点表示的数是0,
故答案为2,0;
∵$\frac{10-(-2)}{10-4}$=2,$\frac{4-(-8)}{-2-(-8)}$=2,
∴【M,N】的暗点表示的数是10;【N,M】的暗点表示的数为-8,
故答案为10,-8;
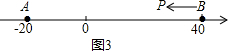
(2)①设运动时间为t秒,则PB=2t,
易得方程2t=2(2t-60).
所以t=60.
②当P是【A,B】的亮点时,∵PA=2PB,
∴2×2t=60-2t,
解得t=10;
当P是【B,A】的亮点时,∵PB=2PA,
∴2t=2(60-2t),
解得t=20;
当A是[B、P]的亮点时,∵AB=2AP,
∴60=2(2t-60)
解得t=45;
当A是[P、B]的亮点时,∵AP=2AB,
∴2t-60=2×60,
解得t=90;
综上所述:当t为10,20,45,90时,P、A、B中恰有一个点为其余两点的亮点.
点评 本题考查了数轴和一元一次方程的应用,明确亮点和暗点的定义,根据定义列出方程是解题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查某条河的河水受污染情况 | B. | 调查一批灯泡的使用寿命 | ||
| C. | 调查某班学生的视力情况 | D. | 调查我国中学生上网情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )| A. | 12.5 | B. | 12 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
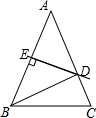 如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
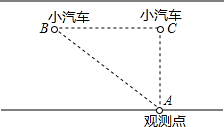 “中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路(盐城到上海段)上的行驶速度不能低于$\frac{50}{3}$米/秒不得超过$\frac{100}{3}$米/秒,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方60米处,过了3秒后,测得小汽车与车速检测仪问的距离变为100米.这辆小汽车行驶速速度符合规定吗?(①符合;②不符合)符合.
“中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路(盐城到上海段)上的行驶速度不能低于$\frac{50}{3}$米/秒不得超过$\frac{100}{3}$米/秒,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方60米处,过了3秒后,测得小汽车与车速检测仪问的距离变为100米.这辆小汽车行驶速速度符合规定吗?(①符合;②不符合)符合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com