练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，△ABC中AB=AC，BD、BE分别是△ABC的高和角平分线，∠C=50°．求∠DBE的大小．
    考点：等腰三角形的性质
    专题：
    分析：首先根据等腰三角形的性质求得∠ABC的度数，然后利用角平分线的性质和高求得∠DBC和∠EBC，从而求得未知的角的度数．
    解答：解：∵AB=AC，C=50°，
    ∴∠ABC=∠C=50°，
    ∵BE是角平分线，
    ∴∠EBC=
    1
    2
    ∠ABC=25°，
    ∵BD是高，
    ∴∠DBC=40°，
    ∴∠DBE=∠DBC-∠EBC=40°-25°=15°．
    点评：本题考查了等腰三角形的性质，解题的关键是求得两个底角的度数，难度不大．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机进校园”现象的看法，统计整理并制作了如下的统计图：

    这次调查的家长总数为（　　）
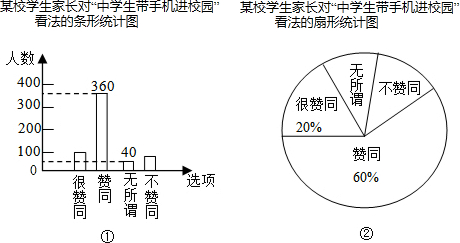
    A、240B、360
    C、600D、1800

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    据统计，2013年十一期间，我市某风景区接待游客的人数为89740人次，用四舍五入法取近似数，将这个数字精确到千位可表示为（　　）
    A、8.9×104
    B、9.0×104
    C、9×104
    D、90000

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：（
    1
    2
    ）-2-
    		12
    -（
    		3
    -2）0；             
    （2）化简：
    m-15
    m2-9
    -
    2
    3-m
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB∥CD，BE平分∠ABC，∠DCB=140°，求∠ABD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：|-4|-
    		9
    +（-2）0；  
    （2）化简：（a-b）2+a（2b-a）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

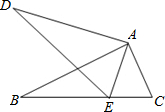    如图，在△ABC和△ADE中，点E在BC边上，∠BAC=∠DAE，∠B=∠D，AB=AD．
    （1）求证：△ABC≌△ADE；
    （2）如果∠AEC=75°，将△ADE绕着点A旋转一个锐角后与△ABC重合，求这个旋转角的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    国道通过A，B两村庄，而C村庄离国道较远，为了响应政府“村村通公路”的号召，C村决定采用自己筹集一部分，政府补贴一部分的方法修建一条水泥路直通国道．已知C村到A，B两村的距离分别为6km，8km，A，B两村距离为10km，那么这条水泥路的最短距离为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    八年级秋游，若租用48座的客车，则正好坐满；若租用64座客车，则能少租用一辆，且有一辆没有坐满，但超过一半．已知租用48座客车每辆250元，租用64座客车每辆300元，问应租用哪种客车合算？

    查看答案和解析>>

    同步练习册答案