
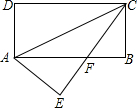
 如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为________.
如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为________.
 ,然后根据三角形的面积公式得到△AFC的面积=
,然后根据三角形的面积公式得到△AFC的面积= •AF•BC=
•AF•BC= •
• •b,化简即可.
•b,化简即可. ,
, •AF•BC
•AF•BC •
• •b
•b .
. .
.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com