
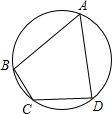
 如图,圆内接四边形ABCD中,∠A=60°,∠B=90°,AD=3,CD=2,则BC=________.
如图,圆内接四边形ABCD中,∠A=60°,∠B=90°,AD=3,CD=2,则BC=________. -1
-1 AD=3
AD=3 ,则EC=3
,则EC=3 -2;又在直角三角形ECB中,BC=
-2;又在直角三角形ECB中,BC= EC,这样就可求出BC.
EC,这样就可求出BC.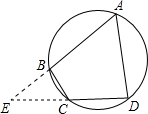 解:延长AB和DC交于点E,如图,
解:延长AB和DC交于点E,如图, AD,而AD=3,所以ED=
AD,而AD=3,所以ED= AD=3
AD=3 ,
, -2;
-2; EC=
EC= (3
(3 -2)=
-2)= -1.
-1. -1.
-1. :2.
:2. 

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com