
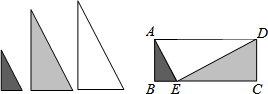
分析 依题意可以得到△ABE∽△ECD∽△DEA,∠B=∠C=∠D=90°,利用相似三角形的性质可以推出BE:CD=AB:EC,而四边形ABCD为矩形,可以得到AB=CD,所以AB2=BE•EC,又CE=3BE,可以得到AB=$\sqrt{3}$BE,由此可以求出BE,CB,最后就可以求出面积.
解答 解:∵形状相同、大小不等的三块直角三角形木板,
∴△ABE∽△ECD∽△DEA,∠B=∠C=∠AED=90°,
∴BE:CD=AB:EC,
∴四边形ABCD为矩形,
∴AB=CD,
∴AB2=BE•EC,
∵CE=3BE,
∴AB=$\sqrt{3}$BE,
∵AE=2,
∴BE=1,AB=$\sqrt{3}$,
∴BC=BE+CE=4BE=4,
∴这个四边形的面积是S=AB×BC=$\sqrt{3}$×4=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了直角三角形的性质和相似三角形的性质,同时也考查了勾股定理,解题时要注意认识图形,难度适中.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
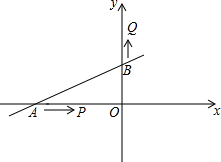 直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒
直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
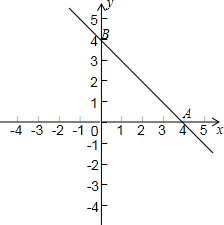 右图是直线y=-x+4在平面直角坐标系中的函数图象,与x轴和y轴的交点分别为点A(4,0)和点B(0,4).
右图是直线y=-x+4在平面直角坐标系中的函数图象,与x轴和y轴的交点分别为点A(4,0)和点B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
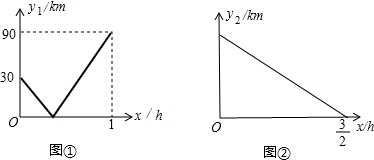
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com