
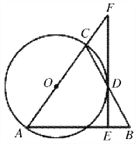
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.
【答案】(1)见解析(2)![]()
【解析】分析:(1)如图,欲证明EF与⊙O相切,只需证得OD⊥EF.
(2)通过解直角△AEF可以求得AF=10.设⊙O的半径为r,由平行线分线段成比例得到![]() ,即
,即![]() ,则易求AB=AC=2r=
,则易求AB=AC=2r=![]() ,所以EB=AB﹣AE=
,所以EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.
详解:(1)证明:如图,连接OD.
∵OC=OD,∴∠OCD=∠ODC.
∵AB=AC,∴∠ACB=∠B,∴∠ODC=∠B,∴OD∥AB,∴∠ODF=∠AEF.
∵EF⊥AB,∴∠ODF=∠AEF=90°,∴OD⊥EF.
∵OD是⊙O的半径,∴EF与⊙O相切;
(2)由(1)知,OD∥AB,OD⊥EF.
在Rt△AEF中,sin∠CFD=![]() ,AE=6,则AF=10.
,AE=6,则AF=10.
∵OD∥AB,∴![]() .
.
设⊙O的半径为r,∴![]() ,解得:r=
,解得:r=![]() ,∴AB=AC=2r=
,∴AB=AC=2r=![]() ,∴EB=AB﹣AE=
,∴EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.
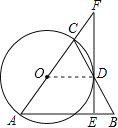


科目:初中数学 来源: 题型:
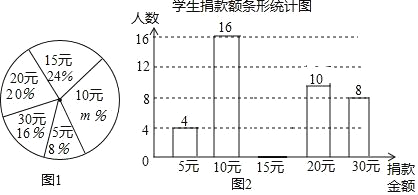
【题目】某校学生会向全校![]() 名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图![]() 中
中![]() 的值是 .
的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为![]() 元的学生人数.
元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
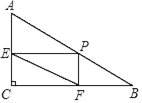
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】缴纳个人所得税是收入达到缴纳标准的公民应居的义务,个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算,新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施,新税法规定个人所得税的免征额为5000元,应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额=税前收总额﹣国家规定扣除专项金额﹣免征额).
级数 | 应纳税所得额 | 税率% |
1 | 不超过3000元的 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
… | … | … |
根据以上信息,解决以下问题:
(1)小明的妈妈应纳税所得额为2000元,她应该缴纳个人所得税______元.
(2)小明的爸爸要缴纳个人所得税590元,他应纳税所得额是多少元?
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额),共要缴纳个人所得税1780元,小明的爸爸应纳税所得额是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | …… |
x x x x | ||||
x x x | y y y | |||
x x | y y | x x x x | ||
图形 | y | x x x | y y y | |
x x | y y | x x x x | ||
x x x | y y y | |||
x x x x |
我们把某格中字母和所得到的多项式称为“特征式多项式”。例如第1格的“特征式多项式”为4x+y。
(1)第3格的“特征式多项式”为________________;
(2)第4格的“特征式多项式”为________________;
(3)第n格的“特征式多项式”为________________;
(4)若第1格的 “特征式多项式”为10,第2格的“特征式多项式”为19,求x、y的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若从 -3,-1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组![]() 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线![]() 上的概率是_________.
上的概率是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com