
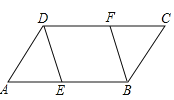
【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
【答案】证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,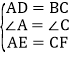 ,
,
∴△ADE≌△CBF(SAS)。
(2)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵AE=CF,∴DF=EB。∴四边形DEBF是平行四边形。
又∵DF=FB,∴四边形DEBF为菱形。
【解析】
试题(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF;
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行四边形,又DF=FB,可根据邻边相等的平行四边形为菱形证出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
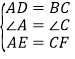 ,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.


科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学从学生入学开始就积极开展环保教育,半学期后随机对部分学生的环保习惯养成情况进行了问卷调查,问卷中的环保习惯有:①随手关灯;②充电后及时拔充电器插头;③生活用水合理重复利用;④不用或少用一次性餐具;⑤少用塑料袋多用环保袋;⑥绿色出行,同学勾选出自己已经养成的环保习惯,学校将结果绘成了如图所示的不完整的条形统计图和扇形统计图.
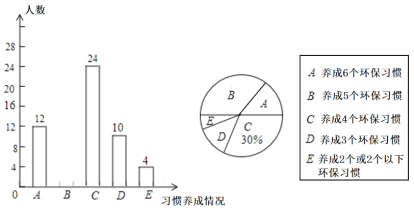
(1)求在这次调查中,一共抽查了多少名学生?
(2)通过计算补全条形统计图.
(3)已知全校共有学生1200人,请估计全校所有学生中已经养成3个或3个以上环保习惯的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=90°,∠COD=20°,OM平分∠AOC,ON平分∠BOD.
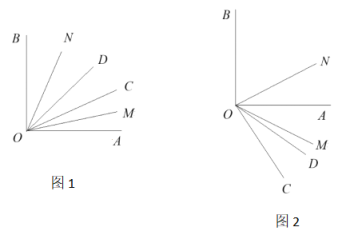
(1)如图1,∠COD在∠AOB内部,且∠AOC=30°.则∠MON的大小为 .
(2)如图1,∠COD在∠AOB内部,若∠AOC的度数未知,是否能求出∠MON的大小,若能,写出你的解答过程;若不能,说明理由.
(3)如图2,∠COD在∠AOB外部(OM在OD上方,∠BOC![]() 180°),试求出∠MON的大小.
180°),试求出∠MON的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列有理数:﹣(﹣3)、﹣4、0、+5、﹣![]()
(1)这些有理数中,整数有 个,非负数有 个.
(2)画数轴,并在数轴上表示这些有理数.
(3)把这些有理数用“<“号连接起来: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com