
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
分析 作EH⊥AD于H,连结OM、CE、OE,如图,设⊙O的半径为R,根据圆周角定理得到∠CEB=90°,再根据切线的性质得OM⊥AD,接着根据等腰梯形的性质得∠ABC=∠A=α,由于∠OEB=∠B=α,则∠OEB=∠A,所以OE∥AD,于是可判断四边形OMHE为正方形,得到HE=OE=R,根据锐角三角函数的定义,在Rt△AEH中得到AE=$\frac{R}{sinα}$,在Rt△BCE中得到BE=2Rcosα,然后计算$\frac{BE}{AE}$的值.
解答 解:作EH⊥AD于H,连结OM、CE、OE,如图,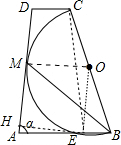 设⊙O的半径为R,
设⊙O的半径为R,
∵BC为直径,
∴∠CEB=90°,
∵AD为⊙O的切线,
∴OM⊥AD,
∵AB∥CD,AD=BC,
∴∠ABC=∠A=α,
∵OB=OE,
∴∠OEB=∠B=α,
∴∠OEB=∠A,
∴OE∥AD,
∴四边形OMHE为矩形,
而OM=OE,
∴四边形OMHE为正方形,
∴HE=OE=R,
在Rt△AEH中,∵sinA=$\frac{HE}{AE}$,
∴AE=$\frac{R}{sinα}$,
在Rt△BCE中,∵cosB=$\frac{BE}{BC}$,
∴BE=2Rcosα,
∴$\frac{BE}{AE}$=$\frac{2Rcosα}{\frac{R}{sinα}}$=2sinαcosα.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.合理构造直角三角形,应用锐角三角函数的定义进行计算是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
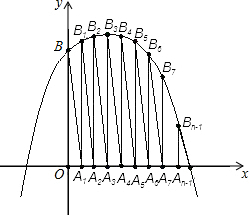 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
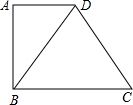 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
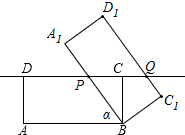 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com